D2.1 Décrire la différence entre des événements indépendants et des événements dépendants, et expliquer la raison pour laquelle leurs probabilités respectives diffèrent en fournissant des exemples.
HABILETÉ : EXPLIQUER LA RAISON POUR LAQUELLE LES PROBABILITÉS D’ÉVÉNEMENTS INDÉPENDANTS ET D’ÉVÉNEMENTS DÉPENDANTS DIFFÈRENT EN FOURNISSANT DES EXEMPLES
Les probabilités d’événements indépendants et dépendants diffèrent, puisque la répétition d’un événement dépendant réduit le nombre total de résultats possibles de l’expérience. La probabilité d’un événement dépend donc du résultat d’un événement précédent, ce qui n’est pas le cas en ce qui concerne les événements indépendants.
Exemple
Présenter aux élèves la situation suivante :
12 billes de couleurs différentes sont insérées dans un sac. Il y a 4 billes bleues, 3 billes vertes et 5 billes rouges. À l’aide d’un diagramme en arbre, détermine les probabilités théoriques de tirer 2 billes rouges successives :
- en remettant la première bille tirée dans le contenant;
- en conservant la première bille tirée.
Compare les deux diagrammes en arbre afin de distinguer les événements indépendants et dépendants.
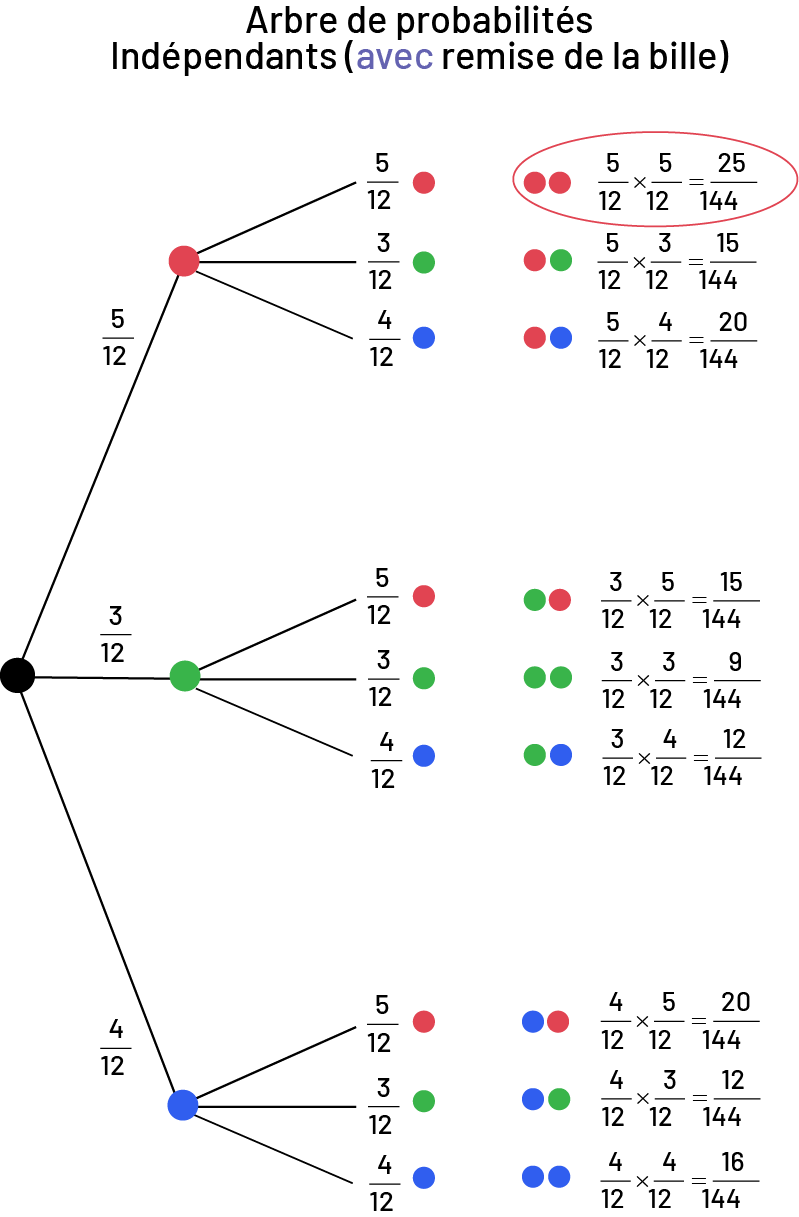Image Arbre de probabilités indépendant, avec remise de la bille. Si à la première pige on a cinq probabilités sur douze de pigner une bille rouge, et qu’à la deuxième pige, on a cinq probabilités sur douze de piger une bille rouge : cinq sur douze multiplié par cinq sur douze égale 25 probabilités sur 144 de piger deux billes rouges. Cette équation est la seule de l’arbre à être encerclée en rouge. Si à la deuxième pige on a trois probabilités sur douze de piger une bille verte : cinq sur douze multiplié par trois sur douze égale 15 probabilités sur 144 de piger une bille rouge puis une bille verte. Si à la deuxième pige on a quatre probabilités sur douze de piger une bille bleue : cinq sur douze multiplié par quatre sur douze égale vingt probabilités sur 144 de piger une bille rouge puis une bille bleue. Si à la première pige on a trois probabilités sur douze de piger une bille verte, et qu’à la deuxième pige, on a cinq probabilités sur douze de piger une bille rouge : trois sur douze multiplié par cinq sur douze égale 15 probabilités sur 144 de piger une bille verte puis une bille rouge. Si à la deuxième pige on a trois probabilités sur douze de piger une bille verte : trois sur douze multiplié par trois sur douze égale neuf probabilités sur 144 de piger deux billes vertes. Si à la deuxième pige on a quatre probabilités sur douze de piger une bille bleue : trois sur douze multiplié par quatre sur douze égale douze probabilités sur 144 de piger une bille verte puis une bille bleue. Si à la première pige on a quatre probabilités sur douze de piger une bille bleue, et qu’à la deuxième pige, on a cinq probabilités sur douze de piger une bille rouge : quatre sur douze multiplié par cinq sur douze égale vingt probabilités sur 144 de piger une bille bleue puis une bille rouge. Si à la deuxième pige on a trois probabilités sur douze de piger une bille verte : quatre sur douze multiplié par trois sur douze égale douze probabilités sur 144 de piger une bille bleue puis une bille verte. Si à la deuxième pige on a quatre probabilités sur douze de piger une bille bleue : quatre sur douze multiplié par quatre sur douze égale seize probabilités sur 144 de piger deux billes bleues
Il y a 25 résultats favorables sur 144 résultats possibles. La probabilité de tirer 2 billes rouges successives est \(\frac{25}{144}\ ou\ 0,17\ ou\ 17\%\).
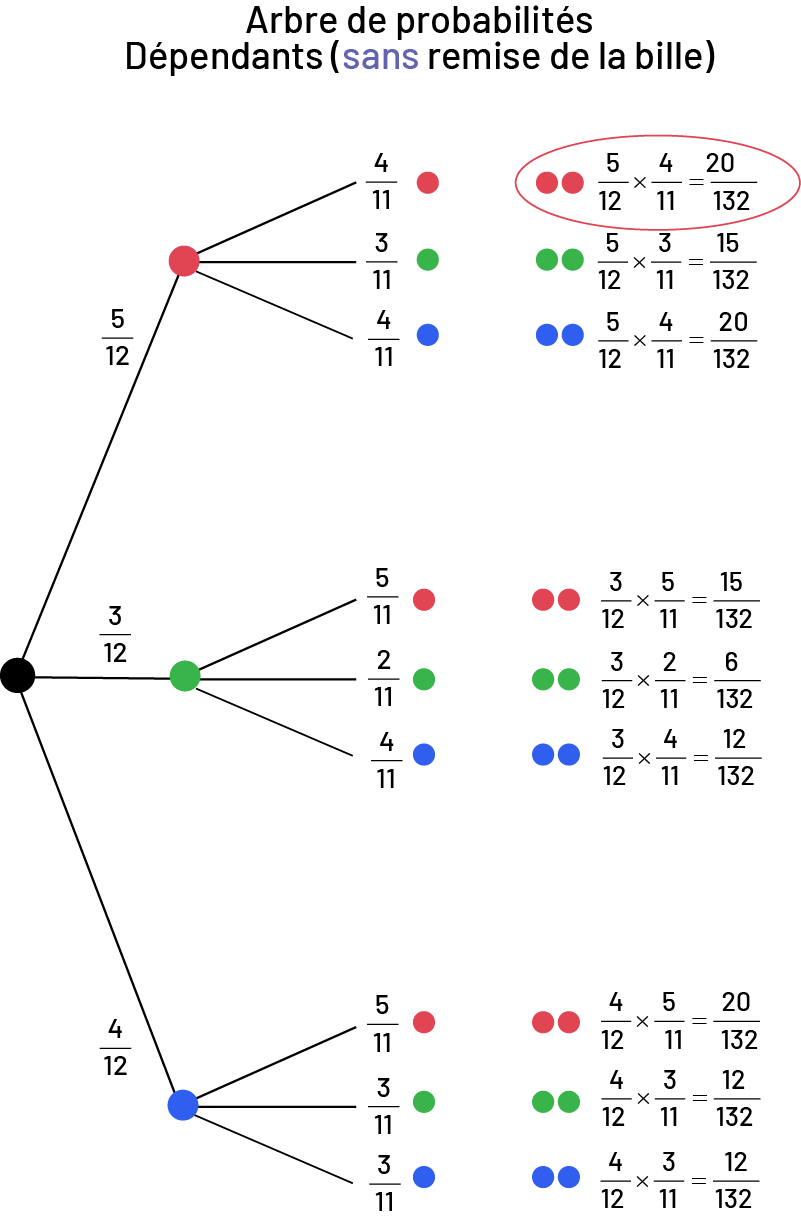Image Arbre de probabilités dépendant, sans remise de la bille. Si à la première pige on a cinq probabilités sur douze de pigner une bille rouge, et qu’à la deuxième pige, on a quatre probabilités sur onze de piger une bille rouge : cinq sur douze multiplié par quatre sur onze égale vingt probabilités sur 132 de piger deux billes rouges. Cette équation est la seule de l’arbre à être encerclée en rouge. Si à la deuxième pige on a trois probabilités sur onze de piger une bille verte : cinq sur douze multiplié par trois sur onze égale 15 probabilités sur 132 de piger une bille rouge puis une bille verte. Si à la deuxième pige on a quatre probabilités sur onze de piger une bille bleue : cinq sur douze multiplié par quatre sur onze égale vingt probabilités sur 132 de piger une bille rouge puis une bille bleue. Si à la première pige on a trois probabilités sur douze de piger une bille verte, et qu’à la deuxième pige, on a cinq probabilités sur onze de piger une bille rouge : trois sur douze multiplié par cinq sur onze égale 15 probabilités sur 132 de piger une bille verte puis une bille rouge. Si à la deuxième pige on a trois probabilités sur onze de piger une bille verte : trois sur douze multiplié par trois sur onze égale neuf probabilités sur 132 de piger deux billes vertes. Si à la deuxième pige on a quatre probabilités sur onze de piger une bille bleue : trois sur douze multiplié par quatre sur onze égale douze probabilités sur 132 de piger une bille verte puis une bille bleue. Si à la première pige on a quatre probabilités sur douze de piger une bille bleue, et qu’à la deuxième pige, on a cinq probabilités sur onze de piger une bille rouge : quatre sur douze multiplié par cinq sur onze égale vingt probabilités sur 132 de piger une bille bleue puis une bille rouge. Si à la deuxième pige on a trois probabilités sur onze de piger une bille verte : quatre sur douze multiplié par trois sur douze égale douze probabilités sur 132 de piger une bille bleue puis une bille verte. Si à la deuxième pige on a quatre probabilités sur onze de piger une bille bleue : quatre sur douze multiplié par quatre sur douze égale seize probabilités sur 132 de piger deux billes bleues.
Il y a 20 résultats favorables sur 132 résultats possibles. La probabilité de tirer 2 billes rouges successives est \(\frac{20}{132}\ ou\ 0,15\ ou\ 15\%\).
Les fractions entre les premiers tirages des deux diagrammes en arbre (indépendants et dépendants) sont identiques. Toutefois, il y a une différence sur le plan des fractions du second tirage dans les deux diagrammes en arbre. Dans celui des événements indépendants, les numérateurs et les dénominateurs ne changent pas. Dans le diagramme en arbre des événements dépendants, les numérateurs et les dénominateurs changent au second tirage, car une des billes n’est jamais remise dans le sac.
Source : En avant, les maths!, 7e année, ML, Données, p. 13-15.