Fondements généraux du domaine Données
Cycle primaire
INTRODUCTION
L’application de concepts liés au traitement des données et à la probabilité est très fréquente dans notre quotidien. En effet, les journaux, les magazines, la radio, la télévision et Internet ont souvent recours aux diagrammes et aux données statistiques pour communiquer une information ou véhiculer un message; par exemple, des réclames publicitaires, des résultats sportifs, des sondages d’opinion, des tendances démographiques, une évaluation des risques pour la santé et des prévisions météorologiques.
Selon Burns (2000, p. 59-61), une connaissance appropriée des concepts liés au traitement des données et à la probabilité est un atout pour les élèves. Les élèves peuvent ainsi :
- se préparer à vivre dans une société de plus en plus axée sur les statistiques;
- éviter d’être induites et induits en erreur par les statistiques;
- développer leur habileté à raisonner;
- diminuer leur incertitude;
- rapporter fidèlement la réalité;
- dissiper certains préjugés;
- formuler convenablement leurs arguments;
- justifier leurs résultats à l’aide de données quantitatives.
Dans le programme-cadre de mathématiques, le traitement des données et la probabilité forment un même domaine. En effet, ces deux sujets sont indissociables, puisque, dans les deux cas, on recueille des données, on les organise, on les analyse et l’on en tire des conclusions. S’il est possible de traiter des données sans avoir recours aux probabilités, le contraire ne l’est pas toujours, les données étant essentielles au calcul des probabilités.
Le personnel enseignant devrait donc privilégier une approche intégrée dans l’enseignement des concepts de données et de probabilité; par exemple, il peut demander aux élèves :
- de classer des objets selon divers attributs;
- de classer certains événements selon les attributs de fréquence, de certitude ou de probabilité;
- de représenter les données recueillies au cours d’une enquête ou d’une expérience de probabilité au moyen d’un tableau ou d’un diagramme, et de les analyser;
- d’utiliser ces données pour répondre à une question d’intérêt et de formuler une conclusion ou une décision en utilisant la terminologie appropriée;
- d’exercer un jugement critique quant aux données recueillies, à leur représentation au moyen d’un diagramme et aux conclusions proposées.
Le traitement des données et la probabilité font habituellement partie de la branche des mathématiques appelée statistique. En statistique, un des principaux objectifs de l’enseignement est d’aider les élèves à analyser des données quantifiables et à prendre des décisions dans des situations impliquant la variabilité.
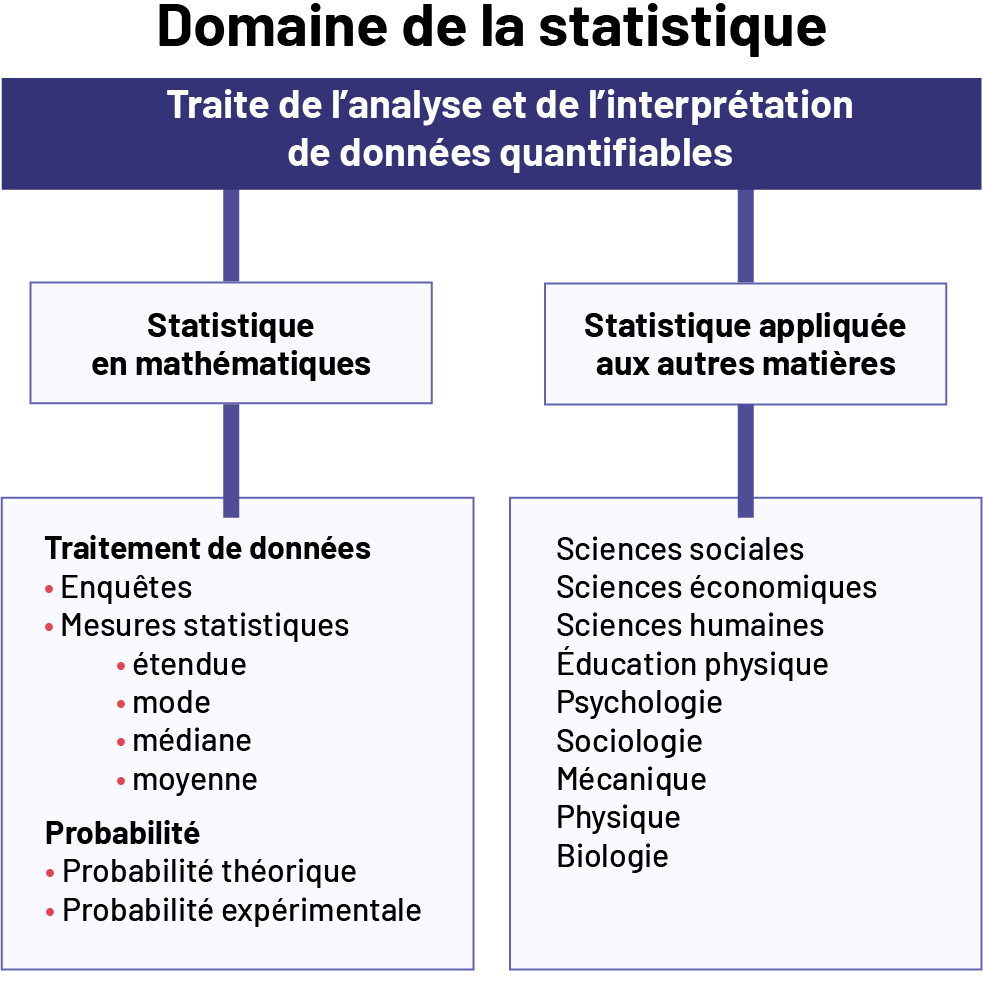 image Titre : Domaine de la statistique; Élément principal : Traite de l’analyse et de l’interprétation de données quantifiables. Deux éléments secondaires liés au premier : Statistique en mathématiques et Statistique appliquée aux autres matières; Sous Statistique en mathématiques : Traitement de données : Enquêtes, Mesures statistiques, étendue, mode, médiane, moyenne. Probabilité : Probabilité théorique, Probabilité expérimentale. Sous Statistique appliquée aux autres matières : Sciences sociales, Sciences économiques, Sciences humaines, Éducation physique, Psychologie, Sociologie, Mécanique, Physique, Biologie.
image Titre : Domaine de la statistique; Élément principal : Traite de l’analyse et de l’interprétation de données quantifiables. Deux éléments secondaires liés au premier : Statistique en mathématiques et Statistique appliquée aux autres matières; Sous Statistique en mathématiques : Traitement de données : Enquêtes, Mesures statistiques, étendue, mode, médiane, moyenne. Probabilité : Probabilité théorique, Probabilité expérimentale. Sous Statistique appliquée aux autres matières : Sciences sociales, Sciences économiques, Sciences humaines, Éducation physique, Psychologie, Sociologie, Mécanique, Physique, Biologie.L’enseignement du domaine Données aux cycles préparatoire et primaire vise, d’une part, à développer les compétences des élèves en matière de littératie statistique et, d’autre part, à développer leur pensée probabiliste. Pour atteindre cet objectif, le personnel enseignant doit présenter aux élèves des situations d’apprentissage authentiques qui font appel au processus d’enquête et qui favorisent l’acquisition de certaines habiletés essentielles. Le schéma ci-dessous illustre l’interaction entre chacun de ces éléments.
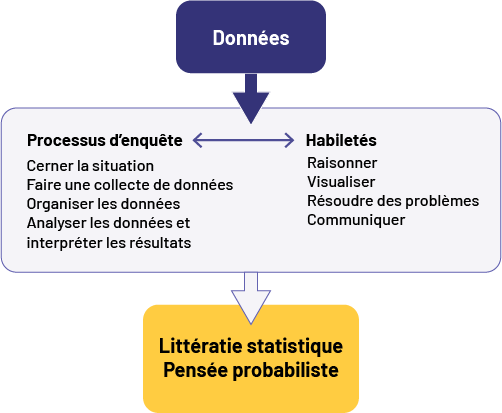 image Premier encadré : Données Flèche pointant vers un autre encadré regroupant deux titres reliés par un droite avec une flèche à chaque extrémité : Processus d’enquête et Habiletés Sous Processus d’enquête : Cerner la situation Faire une collecte de données Analyser les données et interpréter les résultats Sous Habiletés : Raisonner Visualiser Résoudre des problèmes Communiquer Flèche qui part de cet encadré vers un autre encadré comprenant les titres suivants : Littératie statistique Pensée probabiliste.
image Premier encadré : Données Flèche pointant vers un autre encadré regroupant deux titres reliés par un droite avec une flèche à chaque extrémité : Processus d’enquête et Habiletés Sous Processus d’enquête : Cerner la situation Faire une collecte de données Analyser les données et interpréter les résultats Sous Habiletés : Raisonner Visualiser Résoudre des problèmes Communiquer Flèche qui part de cet encadré vers un autre encadré comprenant les titres suivants : Littératie statistique Pensée probabiliste.Dans ce qui suit, on explique chaque élément plus en détail. On présente ensuite le rôle du personnel enseignant dans le contexte d’un enseignement efficace du traitement des données et de la probabilité.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 7-10.
GRANDE IDÉE : LITTÉRATIE STATISTIQUE ET PENSÉE PROBABILISTE
« […] nos stratégies d’enseignement doivent être guidées par une bonne compréhension des concepts clés en traitement des données. Sinon, nous risquons de nous retrouver dans une situation où nos élèves maîtrisent la collecte et la représentation de données, mais sont incapables de s’en servir pour raisonner. » [traduction libre]
(Konold et Higgins, 2003, p. 194)
Aperçu
Les attentes et les contenus d’apprentissage du domaine Données font appel à de nombreux concepts. Leur regroupement sous la grande idée Littératie statistique et pensée probabiliste permet au personnel enseignant de planifier une programmation plus efficace de l’enseignement. Cette grande idée englobe la capacité d’analyser des données statistiques de façon critique et la capacité de déterminer la vraisemblance d’un événement ou d’un résultat.
Grande idée : Littératie statistique et pensée probabiliste
Les activités qui font appel au traitement des données et à la probabilité permettent d'acquérir des compétences en matière de littératie statistique et de développer une pensée probabiliste.
Énoncé 1 :
Les activités de tri et de classement d'objets nous initient au traitement des données et à la probabilité.
Énoncé 2 :
La planification et la réalisation d'une enquête mènent à la collecte et à l'enregistrement de données significatives.
Énoncé 3 :
La représentation de données dans des tableaux et des diagrammes vise à communiquer des renseignements aux fins d'interprétation.
Énoncé 4 :
L'analyse des données permet d'interpréter les résultats et d'en tirer des conclusions pertinentes afin de prendre des décisions réfléchies.
Aux cycles préparatoire et primaire, les élèves aiment bien découvrir leur milieu. Elles et ils sont curieux et se posent toutes sortes de questions au sujet de leurs pairs; par exemple, ce qu’elles et ils aiment, leur âge, leur taille, le nombre de frères et sœurs qu’elles et ils ont, où elles et ils sont nés. Le personnel enseignant peut profiter de cette curiosité naturelle et les inciter à suivre le processus d’enquête pour obtenir des réponses à leurs questions. Ainsi, en partant de situations simples, les élèves acquièrent les compétences de base en matière de littératie statistique, et apprennent progressivement à formuler des questions d’intérêt, puis à recueillir des données, à les organiser, à les représenter et à les analyser.
Les élèves développent aussi une pensée probabiliste tout en apprenant à utiliser certains mots ou certaines expressions servant à décrire la fréquence ou la vraisemblance d’un événement ou d’un résultat. De plus, en suivant le processus d’enquête au cours d’une expérience de probabilité, elles et ils acquièrent une compréhension élémentaire du concept de variabilité.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 34-35.
Le processus d’enquête est une démarche de résolution de problèmes axée sur la collecte et l’analyse de données. Or, les données sont au cœur de toute réflexion liée à la littératie statistique et à la pensée probabiliste. Les élèves auront donc l’occasion de développer leurs compétences en matière de littératie statistique ainsi que leur pensée probabiliste dans la mesure où elles et ils seront exposés à diverses situations qui font appel au processus d’enquête.
Le texte ci-dessous résume les quatre étapes du processus d’enquête. Ces étapes sont décrites plus en détail dans les énoncés 2, 3 et 4 de la grande idée : Littératie statistique et pensée probabiliste.
Étapes du processus d'enquête
- Cerner la situation
- Clarifier le problème.
- Formuler une ou plusieurs questions auxquelles on peut répondre en s'appuyant sur des données.
- Faire une collecte de données
- Élaborer un plan pour recueillir des données pertinentes et appropriées.
- Effectuer la collecte des données selon le plan et les enregistrer.
- Organiser les données
- Regrouper les données recueillies.
- Représenter les données de façon appropriée.
- Analyser les données et interpréter les résultats
- Comparer les données et les combiner.
- Attribuer un sens aux données.
Il est important de noter que ces étapes sont très semblables aux étapes de résolution de problèmes. De plus, ces étapes ne signifient pas nécessairement que le processus est linéaire et séquentiel. En réalité, on va et l’on vient d’une étape à l’autre selon les besoins; par exemple, lorsqu’on interprète les résultats (étape 4) d’une enquête, présentés dans un tableau, on peut envisager qu’une représentation différente de ces résultats pourrait fournir de nouveaux renseignements. On peut alors revenir à l’étape de l’organisation des données (étape 3) et créer le diagramme en question.
On peut même retourner à la question d’intérêt (étape 1) si l’on se rend compte qu’elle n’était pas très précise ou que les résultats ne correspondent pas à l’intention initiale.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 17-18.
« L’utilisation de données authentiques liées à l’expérience personnelle des élèves les motive à apprendre, minimise les conceptions erronées, fonde la formulation d’inférences porteuses de sens et, conséquemment, assure une prise de décision réfléchie. » [traduction libre]
(Connor, Davies et Holmes, 2006, p. 185)
Raisonner, visualiser, résoudre une situation-problème et communiquer sont des habiletés étroitement liées au développement des compétences en matière de littératie statistique et au développement de la pensée probabiliste. Grâce à elles, les élèves peuvent non seulement recueillir et organiser efficacement des données ou décrire des probabilités, mais également les comprendre et les utiliser à bon escient. Le personnel enseignant doit donc continuellement chercher des occasions incitant les élèves à développer ces habiletés et à les utiliser.
HABILETÉ À RAISONNER
L’habileté à raisonner aide les élèves à organiser leur pensée.
« En mathématiques, organiser signifie effectuer des activités mentales telles qu’abstraire, coordonner, différencier, intégrer, construire et structurer. »
(Ministère de l’Éducation du Québec, 2001, p. 128)
En traitement des données, l’habileté à raisonner joue un rôle prépondérant à toutes les étapes du processus d’enquête; par exemple, à l’étape de l’organisation des données (étape 3), les élèves doivent réfléchir à l’objectif de l’enquête, au message qu’elles et ils désirent véhiculer ainsi qu’à la meilleure façon de représenter les données.
Exemple
Le personnel enseignant a encerclé, sur un calendrier, la date de naissance des élèves du groupe-classe. Une ou un élève se demande à quelle saison sont nées et nés la majorité des élèves. Elle ou il décide de mener une enquête au moyen des données existantes. Elle ou il les regroupe par saison et les représente au moyen d’un diagramme à pictogrammes. Avant de créer son diagramme, l’élève doit réfléchir au choix du pictogramme (un gâteau) et de la légende (correspondance un à deux).
 image Diagramme à pictogrammes horizontal, dont le titre est Anniversaires de naissance selon les saisons, le titre de l’axe vertical, Saisons, et le titre de l’axe horizontal, Nombre d’élèves. Il est composé de quatre catégories : Hiver, comptant quatre gâteaux, Automne, comptant deux gâteaux, Été, comptant cinq gâteaux, et Printemps, comptant deux gâteaux. Légende : un gâteau représente deux élèves.
image Diagramme à pictogrammes horizontal, dont le titre est Anniversaires de naissance selon les saisons, le titre de l’axe vertical, Saisons, et le titre de l’axe horizontal, Nombre d’élèves. Il est composé de quatre catégories : Hiver, comptant quatre gâteaux, Automne, comptant deux gâteaux, Été, comptant cinq gâteaux, et Printemps, comptant deux gâteaux. Légende : un gâteau représente deux élèves.
En probabilité, l’habileté à raisonner est aussi très utilisée. Dans toute situation qui relève du hasard, les résultats ne peuvent pas être prédits avec certitude. Il faut donc miser sur le résultat qui a les meilleures chances d’être obtenu. Or, puisqu’il n’est pas toujours facile de déterminer ce résultat, il est tentant de s’en remettre à son intuition.
Aux cycles préparatoire et primaire, le personnel enseignant doit aider les élèves à demeurer objectives et objectifs et à faire appel à leur raisonnement. Pour ce faire, il peut leur présenter des situations simples qui relèvent du hasard, puis leur demander de prédire le résultat et d’expliquer la raison pour laquelle elles et ils font cette prédiction. C’est en justifiant leur prédiction qu’elles et ils développeront leur habileté à raisonner.
Exemple
Le personnel enseignant propose aux élèves de faire tourner deux fois l’aiguille sur la roulette ci-dessous et de noter les résultats. Il leur demande ensuite de prédire le secteur dans lequel va s’arrêter l’aiguille au cours d’un troisième essai et de justifier leur prédiction.
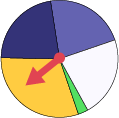
La plupart des élèves reconnaissent intuitivement qu’il est plus probable que l’aiguille s’arrête dans le secteur jaune que dans n’importe quel autre secteur, sans nécessairement être en mesure d’expliquer correctement la raison. Elles et ils auront besoin de réaliser de nombreuses expériences de probabilité avec différentes roulettes pour bien comprendre que, dans cette situation :
- il est plus probable que l’aiguille s’arrête dans le secteur jaune parce que c’est le secteur qui a la plus grande aire;
- les résultats de deux premiers essais n’ont aucune influence sur le résultat du troisième essai.
HABILETÉ À VISUALISER
« L’habileté à visualiser est un processus qui permet à l’élève de se représenter des concepts abstraits sous forme d’images mentales. Ces images lui permettent de manipuler les concepts, de les rendre signifiants et de se les approprier. » [traduction libre]
(Small, 2006, p. 132)
L’habileté à visualiser correspond à la capacité de se faire une image mentale d’une situation ou d’un concept abstrait. Les élèves peuvent ainsi :
- organiser une foule de renseignements sous la forme d’une image mentale;
- utiliser un réseau d’images mentales pour résoudre des problèmes;
- comprendre des concepts et des processus mathématiques en se référant à leur représentation visuelle.
Dans le domaine Données, pour développer l’habileté à créer ces images mentales, les élèves doivent d’abord avoir eu l’occasion de voir, de créer et d’utiliser différentes représentations d’un même concept au cours du processus d’enquête. Le personnel enseignant doit donc s’assurer de les intégrer régulièrement dans les situations d’apprentissage qu’il leur propose.
Exemple 1
Le personnel enseignant construit avec les enfants du jardin d’enfants un diagramme concret pour représenter l’ensemble des fruits que l’on trouve dans les sacs-repas; par exemple, 7 pommes, 4 oranges et 3 bananes. En se faisant une image mentale de ce diagramme, elles et ils peuvent mieux visualiser le fait que l’on trouve la pomme en plus grand nombre que l’orange ou la banane.
Le personnel enseignant peut ensuite leur présenter un diagramme à pictogrammes qui représente les mêmes données. Les enfants pourront mieux comprendre ce nouveau type de diagramme si elles et ils le comparent avec la représentation mentale qu’elles et ils se sont faite du diagramme concret.

 image Diagramme à pictogrammes vertical, dont le titre est Fruits dans les sacs-repas, composé de trois catégories : Pomme, comptant sept pommes, Orange, comptant quatre oranges, et Banane, comptant trois bananes. À la droite de ce diagramme, on voit la tête d’une jeune fille qui pense à ce même diagramme.
image Diagramme à pictogrammes vertical, dont le titre est Fruits dans les sacs-repas, composé de trois catégories : Pomme, comptant sept pommes, Orange, comptant quatre oranges, et Banane, comptant trois bananes. À la droite de ce diagramme, on voit la tête d’une jeune fille qui pense à ce même diagramme.Exemple 2
Chaque jour, pendant une semaine, le personnel enseignant prend en note le nombre de craquelins qu’il y a dans les sacs-repas des élèves. La semaine suivante, il leur présente les résultats à l’aide du diagramme à pictogrammes ci-dessous. La légende indique qu’il y a une correspondance un à quatre entre le pictogramme et le nombre de craquelins.
L’habileté à visualiser amène les élèves à reconnaître que le rectangle rouge représente deux craquelins et que le petit carré rouge en représente un seul.
 image Diagramme à pictogrammes, dont le titre est Nombre de craquelins mangés, composé de cinq catégories : lundi, comptant trois carrés rouges, mardi, comptant quatre carrés rouges et un quart de carré rouge, mercredi, comptant cinq carrés rouges, jeudi, comptant quatre carrés rouges et une moitié de carré rouge, et vendredi, comptant quatre carrés rouges. Légende : un carré rouge représente quatre caquelons.
image Diagramme à pictogrammes, dont le titre est Nombre de craquelins mangés, composé de cinq catégories : lundi, comptant trois carrés rouges, mardi, comptant quatre carrés rouges et un quart de carré rouge, mercredi, comptant cinq carrés rouges, jeudi, comptant quatre carrés rouges et une moitié de carré rouge, et vendredi, comptant quatre carrés rouges. Légende : un carré rouge représente quatre caquelons.
En probabilité, les élèves peuvent aussi recourir à la visualisation pour développer leur compréhension de concepts abstraits.
Exemple
Pour vérifier la compréhension des élèves quant au concept, le personnel enseignant demande d’abord à chaque élève d’indiquer le moyen qu’il préfère pour générer des résultats aléatoires. Les trois réponses les plus fréquentes sont les suivantes : faire tourner l’aiguille d’une roulette, tirer un objet d’un sac et lancer un dé.
Le personnel enseignant leur rappelle que, dans chacune de ces situations, on ne peut prédire avec certitude le résultat, à moins, bien entendu, que les outils en question ne génèrent pas différents résultats de façon aléatoire. Il leur demande d’imaginer la façon dont chacun de ces outils pourrait être fabriqué si on voulait être certain d’obtenir, par exemple, la lettre « h » comme résultat. Les élèves pourraient alors visualiser les outils de la façon suivante.
 image Tête d’une jeune fille qui pense à une roulette divisée en quatre secteurs, chacun contenant la lettre « h » dans un carré mauve. Tête d’une autre jeune fille qui pense à un contenant dans lequel on trouve cinq « h », chacune des lettres dans un carré bleu. Tête d’un jeune garçon qui pense à un cube sur lequel on voit la lettre « h » sur une des faces.
image Tête d’une jeune fille qui pense à une roulette divisée en quatre secteurs, chacun contenant la lettre « h » dans un carré mauve. Tête d’une autre jeune fille qui pense à un contenant dans lequel on trouve cinq « h », chacune des lettres dans un carré bleu. Tête d’un jeune garçon qui pense à un cube sur lequel on voit la lettre « h » sur une des faces.
Les modèles de lignes de fréquence, de certitude et de probabilité décrits ci-après constituent aussi d’excellents moyens visuels pour mieux comprendre des notions de probabilité que véhiculent des mots tels que quelquefois, possible et probable. Chacun de ces mots qualifie un événement ou un résultat sur un continuum qui va de jamais à toujours ou d’impossible à certain. En situant, par exemple, un résultat sur une de ces lignes, on indique de façon approximative si l’on estime que ce résultat est plus près d’une extrémité que de l’autre de ce continuum.

- Les mots jamais, quelquefois, souvent et toujours décrivent la fréquence à laquelle un événement ou un résultat peut se produire.
- La ligne de fréquence représente un continuum. Ses deux extrémités (jamais et toujours) sont des points fixes qui servent d’ancrage.
- Le mot quelquefois décrit la fréquence de tout événement qui peut se produire rarement ou presque jamais.
- Le mot souvent décrit la fréquence de tout événement qui peut se produire presque toujours.
- L’endroit où l’on situe un événement sur la ligne de fréquence indique l’évaluation de la fréquence à laquelle un événement ou un résultat peut se produire.

- Les mots impossible et certain décrivent les deux extrémités du continuum représentant la possibilité que se produise un événement ou un résultat. Ce sont des points fixes qui servent d’ancrage.
- Un événement impossible est un événement qui ne se produit jamais. Un événement certain est un événement qui va toujours se produire.
Note : Les propositions inverses de ces deux propositions ne sont pas nécessairement vraies. Ainsi, dans le contexte d’une expérience, même si un résultat ne s’est jamais produit, cela ne signifie pas qu’il est impossible qu’il se produise. De même, le fait de toujours obtenir un résultat quelconque à la suite d’un certain nombre d’essais n’implique pas nécessairement que l’on est certain de l’obtenir à la suite de tous les essais.
- Le mot possible qualifie tous les événements ou les résultats qui ne sont ni certains ni impossibles.
- L’endroit où l’on situe un événement ou un résultat sur la ligne de certitude reflète l’évaluation de la possibilité que se produise cet événement ou ce résultat.
- Un événement ou un résultat situé au centre de la ligne de certitude est une possibilité qui peut se produire comme ne pas se produire.

- Les mots impossible et certain décrivent les deux extrémités du continuum représentant la probabilité que se produise un événement ou un résultat.
- Le mot probable qualifie tous les événements ou les résultats qui ne sont ni certains ni impossibles.
- Le mot équiprobable qualifie un événement ou un résultat situé au centre de la ligne de probabilité et pour lequel la probabilité qu’il se produise est égale à la probabilité qu’il ne se produise pas.
- L’expression peu probable décrit une probabilité inférieure à 50 %, alors que l’expression très probable décrit une probabilité supérieure à 50 %.
Note : Au cycle primaire, les élèves évaluent de façon intuitive seulement la probabilité que se produise un événement ou un résultat. Ce n’est qu’au cycle moyen qu’elles et ils le feront de façon quantitative à l’aide d’une fraction ou d’un pourcentage.
HABILETÉ À RÉSOUDRE UNE SITUATION-PROBLÈME
Dans le domaine Données, la démarche privilégiée pour résoudre une situation-problème est celle habituellement associée au processus d’enquête. Comme en témoigne le tableau ci-dessous, cette démarche suit pratiquement les mêmes étapes que celles utilisées en résolution de problèmes dans les autres domaines d’étude en mathématiques. Le personnel enseignant doit aider les élèves à faire le lien entre ces étapes.
| Étapes de la résolution de problèmes | Étapes du processus d'enquête |
|---|---|
| Comprendre le problème |
Cerner la situation
|
| Élaborer un plan |
Faire une collecte de données
|
| Mettre le plan en œuvre |
Organiser les données
|
| Vérifier les résultats |
Analyser les données et interpréter les résultats
|
Comme dans les autres domaines en mathématiques, l’apprentissage des concepts du domaine Données doit se faire en situation de résolution de problèmes. Le personnel enseignant doit donc présenter aux élèves des situations engageantes qui les incitent à recourir au processus d’enquête.
Il importe de souligner l’importance accrue du contexte dans le domaine Données. En effet, dans ce domaine, il est pratiquement impossible de résoudre un problème sans tenir compte du contexte; par exemple, en numération et sens du nombre, les élèves peuvent toujours déterminer la somme des nombres 30 et 10 sans que ces nombres soient présentés dans un contexte. Cependant, dans le domaine Données, il leur est impossible d’interpréter et d’utiliser les données 30 et 10 sans connaître ce qu’elles représentent. De même, elles et ils ne pourront interpréter un diagramme à pictogrammes ou un diagramme à bandes si elles et ils ne savent pas à quoi font référence les données représentées en raison du fait que le diagramme n’a pas de titre, pas de légende ou pas d’étiquettes pour définir les catégories.
Note : Pour obtenir d’autres renseignements au sujet du rôle de la résolution de problèmes en mathématiques, consulter le Guide d’enseignement efficace des mathématiques, de la maternelle à la 6e année, fascicule 2 (Ministère de l’Éducation de l’Ontario, 2006, p. 1-75).
HABILETÉ À COMMUNIQUER
« La communication, sous ses multiples formes, est une fenêtre ouverte sur la pensée de l’élève; d’abord, pour comprendre ce qu’elle ou il pense, puis pour évaluer sa compréhension afin de bien orienter l’enseignement. » [traduction libre]
(Small, 2006, p. 178)
L’habileté à communiquer, dans le domaine Données ainsi que dans tous les autres domaines de mathématiques, aide les élèves à exprimer leur compréhension et à clarifier leur pensée. Radford et Demers (2004) soulignent que la communication sous tous ses aspects est un moyen de transformation du savoir et qu’apprendre revient à s’approprier ce savoir.
Le personnel enseignant doit favoriser un climat d’engagement au dialogue au sein du groupe-classe. Pour ce faire, il doit présenter des situations d’apprentissage d’envergure qui font en sorte que les échanges entre les élèves sont nécessaires pour arriver à comprendre le problème et trouver une solution. La communication, qu’elle soit orale ou écrite, doit faire appel aux symboles, à la terminologie et aux représentations graphiques appropriées, ainsi qu’à des raisonnements et à des arguments mathématiques qui mettent en évidence les concepts visés. Aux cycles préparatoire et primaire, la communication orale est un préalable à la communication écrite.
Communication orale
Les élèves doivent apprendre à utiliser la communication orale pour atteindre divers objectifs. En questionnant les élèves, le personnel enseignant peut susciter des discussions qui visent un objectif en particulier. Le tableau ci-dessous en donne quelques exemples.
| Objectif | Questionnement |
|---|---|
| Relater des expériences antérieures pertinentes |
Qu'avez-vous observé dans les diagrammes? Comment ont-ils été créés? Auriez-vous les mêmes résultats si vous répétiez cette expérience 10 autres fois? |
| Formuler et expliquer une prédiction |
Pensez-vous qu'il y aura plus d'élèves à l'épreuve des 200 m qu'à la course à obstacles? Justifiez votre réponse. Croyez-vous qu'il est plus probable que l'aiguille s'arrête dans le secteur rouge de la roulette que dans le secteur bleu? Pourquoi? |
| Comparer différentes stratégies ou idées |
Parmi la liste de questions, choisissez-en une pour effectuer votre sondage. Justifiez votre choix. Pour réaliser cette expérience de probabilité, est-il plus approprié d'utiliser une roulette ou un dé? |
| Partager une tâche | Quel est le rôle de chacun des membres de votre équipe? |
| Discuter des relations, des ressemblances ou des différences |
Quelles sont les ressemblances et les différences entre ces deux tableaux? Quel rapport y a-t-il entre la fréquence de ce résultat et la fréquence de chacun des deux autres résultats? |
| Justifier |
Pourquoi avez-vous choisi cette légende? Pourquoi dites-vous qu'il y a probablement plus de billes bleues que de billes rouges ou de billes jaunes dans le sac? |
| Expliquer |
Quelle démarche avez-vous suivie pour recueillir vos données et les enregistrer? Quelles modifications devrait-on apporter à ce diagramme? |
Dans un contexte de probabilité, l’acquisition d’une certaine terminologie contribue grandement au développement de la pensée probabiliste. Au début, les élèves ont tendance à décrire la probabilité d’un événement en utilisant un vocabulaire usuel; par exemple, elles et ils diront : « Je mange du spaghetti tous les vendredis soir. C’est tout le temps comme ça. » ou « Je joue à la marelle presque tous les jours. » Le personnel enseignant doit les aider à acquérir et à utiliser une terminologie liée à la fréquence; par exemple, « Je mange toujours du spaghetti le vendredi soir. » ou « Je joue souvent à la marelle. ». Au fil des ans viendront s’ajouter d’autres termes de probabilité tels que certain, impossible, peu probable, équiprobable et très probable.
Pour aider les élèves à acquérir le vocabulaire lié au traitement des données et à la probabilité, le personnel enseignant peut préparer un mur de mots (voir le Guide d’enseignement efficace des mathématiques, de la maternelle à la 6e année, fascicule 3, ministère de l’Éducation de l’Ontario, 2006). Les lignes de fréquence, de certitude et de probabilité constituent aussi d’excellents outils visant à faciliter l’acquisition du vocabulaire lié à la probabilité.
Communication écrite
Consigner ses idées par écrit est habituellement plus difficile que de les exprimer oralement, surtout pour les élèves des cycles préparatoire et primaire qui commencent à apprendre à écrire. Toutefois, il y a des situations où le contraire est vrai; par exemple, elles et ils peuvent représenter un ensemble de données statistiques de façon beaucoup plus succincte et efficace à l’aide d’un tableau ou d’un diagramme qu’à l’aide d’une description orale. Elles et ils doivent cependant apprendre à utiliser correctement les diverses représentations conventionnelles des données, comme le tableau de fréquences, le diagramme à pictogrammes et le diagramme à bandes, afin de s’assurer que le message transmis est le bon et qu’il est bien compris par les autres. Elles et ils peuvent ensuite utiliser ces représentations pour justifier un raisonnement ou appuyer un argument au cours d’un échange mathématique en groupe-classe.
Dans le domaine Données, les élèves ont de multiples occasions d’utiliser la communication écrite pour présenter les résultats d’une enquête ou exprimer leur pensée. En voici quelques exemples :

Note : Pour obtenir d’autres renseignements au sujet du rôle de la communication orale et de la communication écrite en mathématiques, consulter le Guide d’enseignement efficace des mathématiques, de la maternelle à la 6e année, fascicule 2 (Ministère de l’Éducation de l’Ontario, 2006).
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 18-31.
« La base d’un enseignement efficace en mathématiques repose sur l’habileté du personnel enseignant à créer un environnement propice à la communication et à utiliser l’information qui ressort du partage des réflexions mathématiques des élèves. […] Le rôle du personnel enseignant est donc d’utiliser des stratégies d’enseignement qui incitent les élèves à parler de mathématiques. Il lui revient aussi d’alimenter ce dialogue en posant des questions précises pour mettre en évidence tel élément de procédure, pour clarifier tel point de discussion ou pour aider les élèves à exprimer ou à justifier leur point de vue. »
(adapté de Ministère de l’Éducation de l’Ontario, Guide d’enseignement efficace des mathématiques, de la maternelle à la 6e année, fascicule 2, 2006, p. 80)
Les élèves ont besoin de direction et d’encadrement pour apprendre à résoudre des problèmes liés au traitement des données et à la probabilité. Le personnel enseignant doit avoir une vue d’ensemble du parcours que doivent suivre les élèves et planifier les activités d’apprentissage en conséquence. Il doit déterminer les situations où il est important de recourir à l’enseignement explicite en s’assurant de modeler sa démarche, ses interrogations et son raisonnement.
Le personnel enseignant doit aussi :
- proposer aux élèves une variété de situations d’apprentissage engageantes à un degré de difficulté approprié;
- encourager les élèves à utiliser du matériel concret et semi-concret;
- s’assurer que les élèves utilisent de façon appropriée la terminologie relative au traitement des données et à la probabilité;
- mettre l’accent sur la compréhension des concepts;
- poser des questions aidant les élèves à franchir une certaine étape ou les incitant à réfléchir et à clarifier leur pensée.
Un enseignement efficace dans le domaine Données implique aussi chez les élèves le développement simultané de la pensée probabiliste et des compétences en matière de littératie statistique. Il importe donc d’aider les élèves à établir des liens entre les concepts relatifs aux données et ceux relatifs à la probabilité. Pour ce faire, le personnel enseignant doit choisir des situations d’apprentissage dans lesquelles elles et ils pourront établir ces liens; par exemple, les élèves devront déterminer la probabilité d’un événement à partir de données issues d’une enquête (exemple 1) ou suivre certaines des étapes du processus d’enquête à partir de données issues d’une expérience de probabilité (exemple 2).
Exemple 1
Chacune ou chacun des élèves du groupe-classe révèle le mois de son anniversaire de naissance. Elles et ils créent ensuite un diagramme à bandes pour représenter ces données. Une fois l’analyse des données et l’interprétation des résultats terminées, le personnel enseignant met tous les prénoms des élèves dans un sac. Il leur demande d’utiliser le diagramme pour décrire la probabilité de tirer le prénom d’une ou d’un élève dont l’anniversaire est en août.
(Selon les données que représente le diagramme, il est peu probable de tirer le prénom d’une ou d’un élève dont l’anniversaire est en août.)
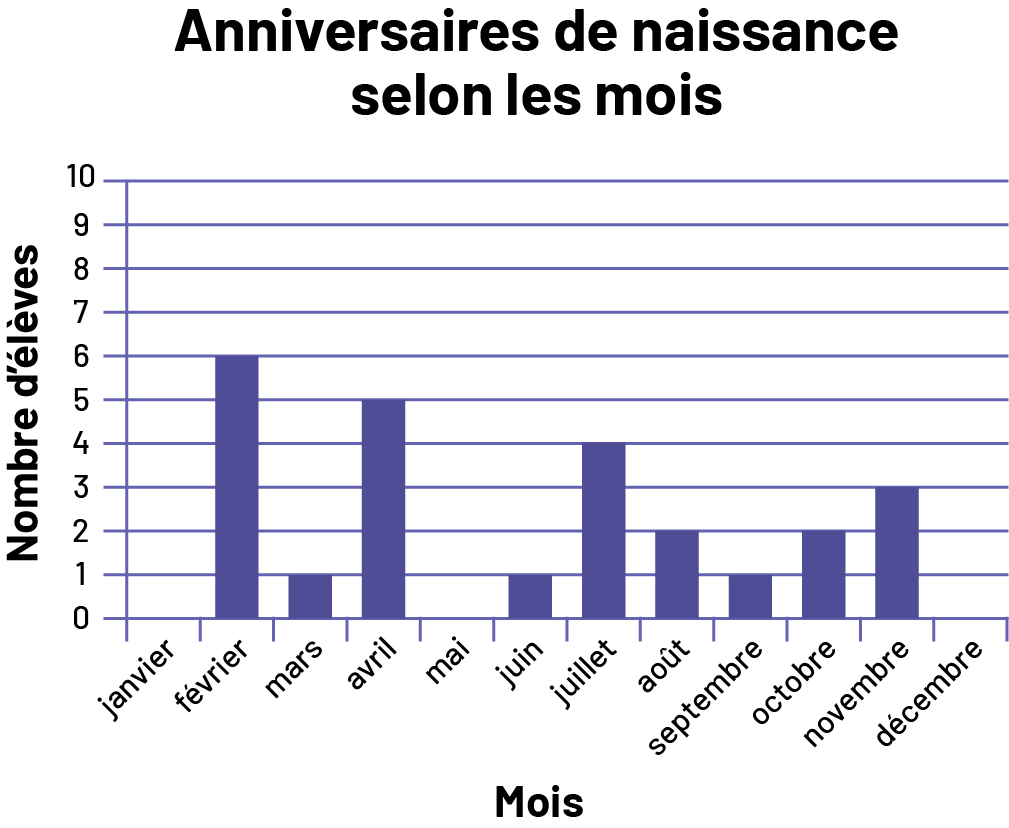 image Le diagramme à bandes s’intitule « Anniversaires de naissance selon les mois ». L’axe vertical correspond aux mois tandis que l’axe vertical, gradué de zéro à dix, correspond au nombre d’élèves. Il n’y a aucune bande en janvier. En février, la bande s’élève à six. En mars, la bande s’élève à un. En avril, la bande s’élève à cinq. En mai, il n’y a aucune bande. En juin, la bande s’élève à un. En juillet, la bande s’élève à quatre. En août, la bande s’élève à deux. En septembre, la bande s’élève à un. En octobre, la bande s’élève à deux. En novembre, la bande s’élève à trois. Et en décembre, il n’y a aucune bande.
image Le diagramme à bandes s’intitule « Anniversaires de naissance selon les mois ». L’axe vertical correspond aux mois tandis que l’axe vertical, gradué de zéro à dix, correspond au nombre d’élèves. Il n’y a aucune bande en janvier. En février, la bande s’élève à six. En mars, la bande s’élève à un. En avril, la bande s’élève à cinq. En mai, il n’y a aucune bande. En juin, la bande s’élève à un. En juillet, la bande s’élève à quatre. En août, la bande s’élève à deux. En septembre, la bande s’élève à un. En octobre, la bande s’élève à deux. En novembre, la bande s’élève à trois. Et en décembre, il n’y a aucune bande.
Exemple 2
Le personnel enseignant demande aux élèves de réaliser une expérience de probabilité et de noter les résultats dans un tableau. (Voir la situation d’apprentissage de 2e année, Il faut un nom à notre mascotte!)
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 31-33.
ÉCHANGE MATHÉMATIQUE
L’échange mathématique est un temps d’objectivation, pendant ou après l’apprentissage, qui va au-delà du simple échange d’idées et de stratégies qu’utilisent les élèves. Au cours de l’échange, les élèves cherchent à défendre leurs idées et à convaincre les autres du bien-fondé de leurs stratégies et de leurs solutions.
L’échange mathématique est un moment pédagogique fort au cours duquel le personnel enseignant dirige les discussions de façon stratégique afin de faire ressortir des idées mathématiques importantes. Celui-ci se prête bien à une approche pédagogique fondée sur la vision que les élèves forment une communauté d’apprentissage.
Points à considérer
- Afin de faciliter la discussion pendant l’échange mathématique, organiser une aire de rencontre. Les élèves pourront y échanger des idées et présenter des exposés en renforçant leur sentiment d’appartenance à la communauté. L’aire de rencontre doit :
- être spacieuse et bien définie pour que les élèves puissent s’y rassembler pour échanger, discuter et faire des présentations;
- être assez grande pour que chaque élève puisse bouger ou remuer un peu sans déranger les autres;
- être éloignée des étagères de rangement, qui pourraient être une source de distraction pendant la rencontre;
- être près des référentiels pour s’y référer, au besoin;
- être près des outils de présentation.
- Au cours de l’exploration, le personnel enseignant circule parmi les élèves, observe la démarche des équipes et écoute leurs discussions. Ses observations lui permettent de choisir l’ordre des présentations en vue de l’échange. Ce choix est guidé par l’objectif qu’il s’est fixé, comme l’application d’une stratégie et l’utilisation d’un modèle mathématique, pour assurer la compréhension des concepts.
- La présentation du travail de chaque élève n’est pas nécessaire; il est préférable de se limiter à présenter les démarches ou les solutions qui se distinguent. Demander aux élèves de montrer leur solution ou leur démarche si elle est semblable à celle présentée, sans toutefois l’expliquer. S’assurer de choisir des élèves différentes et différents d’un échange à l’autre.
- Pendant l’échange, inviter chaque membre de l’équipe à présenter sa réflexion quant au travail accompli après avoir préparé des arguments clairs et convaincants.
- Pendant l’échange, inviter les élèves à poser des questions sur la démarche et les explications de celles et de ceux qui font une présentation. Ce questionnement favorise la vérification de leur propre compréhension et fait en sorte que les présentatrices et les présentateurs ajustent, elles et eux aussi, leur compréhension.
- Créer, dans la salle de classe, un climat de confiance et de respect où toutes et tous les élèves sont encouragés à prendre part aux activités et où tous les propos sont valorisés; par exemple, une ou un élève doit se sentir à l’aise de présenter une erreur dans son travail à titre de contre-exemple qui aidera à la compréhension de toutes et de tous.
- Poser aux élèves des questions stratégiques afin de les aider à bâtir une bonne compréhension des concepts. En voici quelques exemples :
- Quelqu’un peut-il résumer l’idée présentée?
- Comment as-tu procédé pour...?
- Comment as-tu surmonté cette difficulté?
- Pourquoi as-tu employé cette stratégie?
Pour obtenir de plus amples renseignements au sujet de l’échange mathématique, consulter le Guide d’enseignement efficace des mathématiques, de la maternelle à la 6e année, fascicule 3 (Ministère de l’Éducation de l’Ontario, 2006).
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 283-284.
