D1.1 Expliquer pourquoi des pourcentages sont utilisés pour représenter la distribution d’une variable provenant d’une population ou d’un échantillon dans de grands ensembles de données, et fournir des exemples.
Habileté : expliquer la raison pour laquelle des pourcentages sont utilisés pour représenter la distribution d’une Variable
Il est plus facile de comparer des catégories en faisant la comparaison des valeurs relatives, comme les pourcentages, plutôt que des valeurs absolues. Imaginons, par exemple, que, dans un sondage effectué auprès de 65 000 touristes, 6 323 personnes disent avoir visité des bâtiments historiques et 7 247 personnes disent avoir visité un musée. À première vue, le musée semble beaucoup plus populaire que les bâtiments historiques puisqu’il y a près de 1 000 personnes de plus qui l’ont visité. Toutefois, il est plus facile de comparer des valeurs relatives. Dans ce cas-ci, 10 % des touristes ont visité des bâtiments historiques comparativement à 11 % qui ont visité un musée. On peut donc dire que les deux choix sont aussi populaires l’un que l’autre.
Endroits visités par les touristes
| Endroits visités | Fréquence |
|---|---|
| Musées | 7 247 |
| Plages | 12 452 |
| Parcs | 9 562 |
| Cinémas | 3 625 |
| Restaurants | 8 982 |
| Hôtels | 11 645 |
| Sentiers pédestres | 5 164 |
| Bâtiments historiques | 6 323 |
| Total | 65 000 |
Tableau de fréquences relatives
Endroits visités par les touristes
| Endroits visités par les touristes | Fréquence | Fréquence relative (fractions) | Fréquence relative (nombres décimaux) | Fréquence relative (%) |
|---|---|---|---|---|
| Musées | 7 247 | \(\frac{7\ 247}{65\ 000}\) | 0,11 | 11 % |
| Plages | 12 452 | \(\frac{12\ 452}{65\ 000}\) | 0,19 | 19 % |
| Parcs | 9 562 | \(\frac{9\ 562}{65\ 000}\) | 0,14 | 14 % |
| Cinémas | 3 625 | \(\frac{3\ 625}{65\ 000}\) | 0,06 | 6 % |
| Restaurants | 8 982 | \(\frac{8\ 982}{65\ 000}\) | 0,14 | 14 % |
| Hôtels | 11 645 | \(\frac{11\ 645}{65\ 000}\) | 0,18 | 18 % |
| Sentiers pédestres | 5164 | \(\frac{5\ 164}{65\ 000}\) | 0,08 | 8 % |
| Bâtiments historiques | 6 323 | \(\frac{6\ 323}{65\ 000}\) | 0,10 | 10 % |
| Total | 65 000 | \(\frac{65\ 000}{65\ 000}\) | 1,00 | 100 % |
Note : Puisque toutes les autres fréquences relatives ont été arrondies vers le haut, la fréquence relative de la catégorie “Parcs” a été arrondie à la baisse afin d’équilibrer les données et d’obtenir un total vraisemblable de 100 %.
Diagramme circulaire
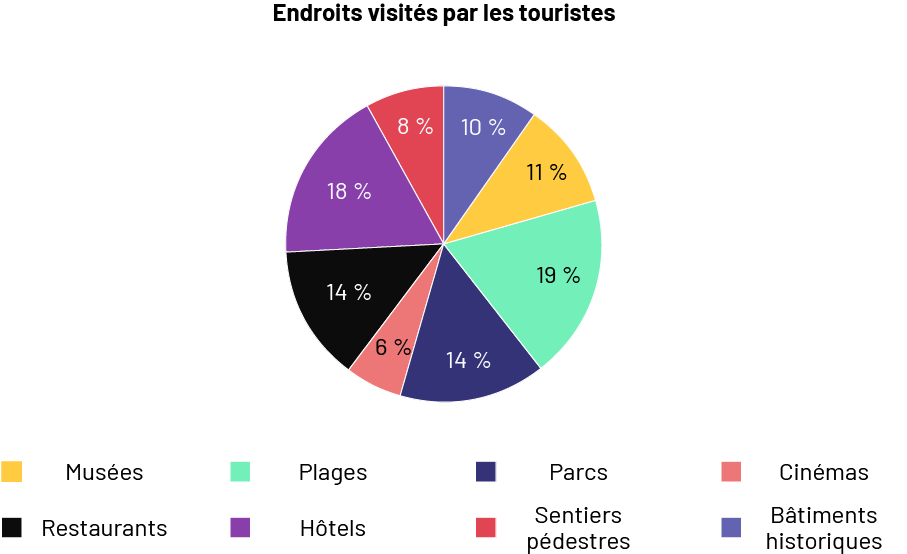
Habileté : donner des exemples afin d’expliquer ou de justifier l’utilisation de pourcentages
Voici un exemple qui justifie la raison pour laquelle il est préférable de choisir les pourcentages lorsque les nombres de la colonne Fréquence sont élevés.
Le ministère de l’Environnement, de la Protection de la nature et des Parcs cherche à déterminer si les citoyennes et citoyens de la ville de Toronto empruntent des moyens de déplacement écologiques pour réduire leur empreinte carbone. Un sondage a été mené auprès d’un échantillon de 88 500 individus âgés de 25 ans à 35 ans habitant à Toronto. Les données recueillies lors du sondage ont été représentées dans un tableau de fréquences ainsi que dans un diagramme circulaire.
Tableau de fréquences
Moyens de déplacement qu'utilisent les citoyennes et citoyens de 25 à 35 ans, à Toronto
| Moyens de déplacement | Fréquence |
|---|---|
| Voiture | 35 209 |
| Covoiturage | 4 235 |
| Autobus de ville | 17 121 |
| Vélo | 8 754 |
| À pied | 2 420 |
| Métro | 20 761 |
| Total | 88 500 |
Diagramme circulaire
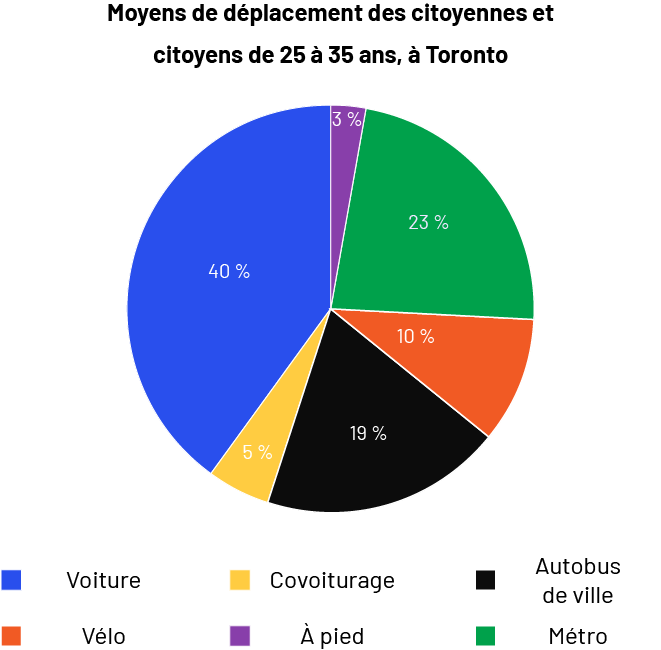
Le tableau de fréquences donne une idée globale de la façon dont sont distribuées les données, mais n’offre pas l’avantage de comparer facilement les données entre elles, comme le fait le diagramme circulaire. Celui-ci présente les fréquences relatives exprimées en pourcentages, de sorte qu’il est possible d’analyser les données rapidement. Le tableau de fréquences permet de lire, par exemple, que 35 209 individus utilisent leur propre voiture et que 4 235 individus font du covoiturage pour se déplacer. Ces mêmes données sont beaucoup plus faciles à interpréter en comparant des pourcentages, en disant que 40 % des individus utilisent leur propre voiture et que 5 % font du covoiturage. Il est ainsi plus facile d’interpréter la distribution des données.
Source : En avant, les maths!, 7e année, ML, Données, p. 6-7.
Connaissance : population
Dans le domaine Données, l’ensemble des objets, des événements ou des individus à étudier est appelé la population. Au cours de la planification de la collecte de données, il faut d’abord définir la population cible de l’enquête, c’est-à-dire le groupe d’individus ou d’objets que vise l’enquête. Le choix de la population est, en partie, dicté par l’intention de l’enquête et l’énoncé de la question d’intérêt.
Exemples de populations
• Les habitantes et habitants du Canada
• Les amatrices et amateurs de baseball
• Les élèves de 7e année de l’école
• Les élèves du cycle intermédiaire
• Les parents des élèves du cycle intermédiaire
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 52.
Connaissance : échantillon représentatif d’une population
Dans le domaine Données, l’ensemble des objets, des événements ou des individus à étudier est appelé la population. La fraction de la population observée, mesurée ou sondée est appelée l’échantillon.
À partir de la 5e année, les enquêtes peuvent porter sur une population dont la taille est telle qu’il est habituellement impossible de l’interroger, de la mesurer ou de l’observer en entier. Les élèves doivent alors mener leur enquête auprès d’une partie de cette population seulement. Ce sous-groupe, appelé l’échantillon, doit être représentatif de la population que vise l’enquête. En mathématiques, le choix d’un échantillon est régi par des normes statistiques complexes, basées sur des concepts de probabilité, qui assurent la validité et la fiabilité des résultats. Aux cycles moyen et intermédiaire, les élèves n’ont pas à se préoccuper de ces normes; il leur suffit de développer une compréhension intuitive de ce qui pourrait être, pour les besoins de l’enquête, un échantillon représentatif de la population cible.
L’idée que les résultats d’une enquête faite auprès d’un groupe restreint puissent refléter la réalité d’une plus grande population n’est pas nécessairement facile à concevoir. Les élèves doivent comprendre que l’échantillon fait partie d’un tout et que, même une petite partie de la population, lorsqu’elle est bien sélectionnée, donne une bonne idée du tout. Au cycle moyen, elles et ils commencent à assimiler ce concept de façon informelle. Si certaines et certains en ont une compréhension intuitive, d’autres ont de fausses conceptions qu’il importe de corriger.
L’échantillon fait en sorte de tirer des conclusions et de faire des généralisations concernant la population en entier sans devoir interroger l’ensemble de celle-ci. Toutefois, ces conclusions sont valides, uniquement si l’échantillon est représentatif de l’ensemble de la population cible.
Exemples de fausses conceptions
- L’échantillonnage ne fonctionne pas parce qu’il est impossible de tenir compte de toutes les différentes caractéristiques de la population (variabilité).
- Pour être juste, il faut toujours avoir le même nombre d’individus dans chacune des catégories.
- Les résultats ne sont pas bons, car nous n’avons pas interrogé tout le monde.
Au cours de la planification de la collecte de données, les élèves doivent avoir une compréhension intuitive des liens qui existent entre la représentativité d’un échantillon relativement à la population et les trois facteurs suivants : la taille de l’échantillon, le processus de sélection et le processus de stratification.
Taille de l’échantillon
Pour que les résultats de l’enquête soient représentatifs de la population, il faut tenir compte de la taille de l’échantillon. Le personnel enseignant doit aider les élèves à trouver un juste milieu entre un échantillon trop grand et un échantillon trop petit.
Processus de sélection
Échantillonnage aléatoire simple
Les élèves doivent comprendre qu’une des meilleures façons d’avoir un bon échantillon libre de biais est de le choisir de façon aléatoire, c’est-à-dire de façon que tous les individus aient les mêmes chances d’en faire partie.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 52-55.
Échantillonnage aléatoire systématique
L’échantillonnage aléatoire systématique est utilisé lorsque les sujets d’une population sont sélectionnés selon une approche systématique déterminée de manière aléatoire; par exemple, un échantillon pourrait être déterminé à partir d’une liste alphabétique de noms, en utilisant un nom de départ et un nombre, par exemple, un nom sur quatre, sélectionné au hasard.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Processus de stratification
Dans certaines enquêtes, on pourrait vouloir s’assurer que certains sous-groupes de la population sont bien représentés dans l’échantillon. On dit alors que la population est stratifiée (divisée en groupes mutuellement exclusifs) et l’on veut que chaque strate (groupe) soit représentée dans l’échantillon.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 56.
Échantillonnage aléatoire stratifié
L’échantillonnage aléatoire stratifié consiste à diviser la population en strates, puis à prélever un échantillon aléatoire de chacune d’elles; par exemple, une population scolaire pourrait être divisée en deux sous-populations (strates) : l’une avec les élèves qui prennent l’autobus pour aller à l’école et l’autre avec celles et ceux qui ne le prennent pas. Ensuite, un sondage pourrait être mené auprès de 10 % de la population choisie au hasard dans chacune de ces strates.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Connaissance : pourcentage
Rapport exprimé au moyen du symbole de pourcentage : %. Le mot pourcentage signifie « sur cent »; par exemple, 30 % signifient 30 sur 100. Un pourcentage peut être représenté à l’aide d’une fraction ayant un dénominateur de 100; par exemple, \(30\% = \frac{30}{100}\).
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : VARIABLE
Tout attribut, tout nombre ou toute quantité qui peut être mesuré ou dénombré.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Connaissance : ensembles de données
Groupe de données interreliées.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
