D2.2 Déterminer et comparer les probabilités théoriques et expérimentales que deux événements indépendants se produisent.
ACTIVITÉ 1 : SITUATION COMPRENANT DEUX CHOIX SUCCESSIFS
Présenter aux élèves la situation suivante :
Véronique aimerait faire une activité avec une de ses amies. Elle hésite entre demander à Amélie, à Julie, à Sophie ou à Fanny, et elle hésite entre aller au parc, faire du vélo ou aller à la piscine. Si elle décide de choisir l’amie et l’activité au hasard, quelle est la probabilité que Véronique :
- se rende à la piscine avec Julie?
- fasse une activité avec Fanny?
- fasse du vélo?
Les élèves peuvent dessiner deux roulettes pour mieux visualiser la situation.
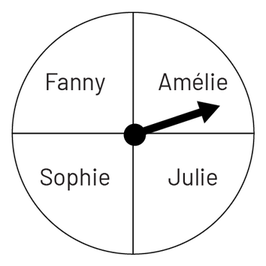
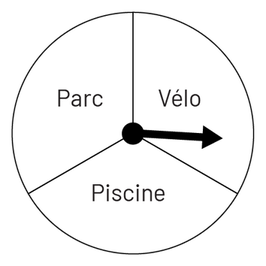 Deux images de roulettes blanches munies d’une aiguille sont placées côte à côte. La première est
séparée en 4 parties possédant respectivement les noms suivants : Fanny, Amélie, Sophie, Julie. L’aiguille pointe
dans la section d’Amélie. La deuxième roulette est séparée en trois parties, respectivement nommées parc, vélo,
piscine. L’aiguille pointe dans la section vélo.
Deux images de roulettes blanches munies d’une aiguille sont placées côte à côte. La première est
séparée en 4 parties possédant respectivement les noms suivants : Fanny, Amélie, Sophie, Julie. L’aiguille pointe
dans la section d’Amélie. La deuxième roulette est séparée en trois parties, respectivement nommées parc, vélo,
piscine. L’aiguille pointe dans la section vélo.On s’intéresse à la probabilité des résultats combinés lorsqu’on fait tourner les deux flèches. Il faut d’abord déterminer et énumérer les résultats équiprobables possibles. Si la première flèche s’arrête sur le nom Amélie, la deuxième flèche peut s’arrêter sur l’activité Parc, Vélo ou Piscine. La même chose se produit si la première flèche s’arrête sur le nom Julie, Sophie ou Fanny. On voit rapidement qu’il y a 12 résultats équiprobables et on peut les représenter à l’aide :
d’un diagramme en arbre;
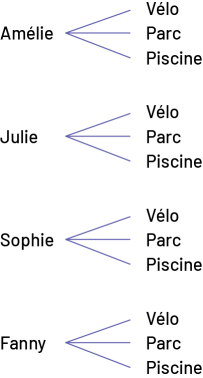
d’un tableau;
| Vélo | Parc | Piscine | |
|---|---|---|---|
| Amélie | Vélo avec Amélie | Parc avec Amélie | Piscine avec Amélie |
| Julie | Vélo avec Julie | Parc avec Julie | Piscine avec Julie |
| Sophie | Vélo avec Sophie | Parc avec Sophie | Piscine avec Sophie |
| Fanny | Vélo avec Fanny | Parc avec Fanny | Piscine avec Fanny |
d’une liste ordonnée.
Amélie et vélo, parc, piscine
Julie et vélo, parc, piscine
Sophie et vélo, parc, piscine
Fanny et vélo, parc, piscine
Vélo avec Amélie, Julie, Sophie ou Fanny
Parc avec Amélie, Julie, Sophie ou Fanny
Piscine avec Amélie, Julie, Sophie ou Fanny
Peu importe la représentation utilisée, les élèves peuvent ensuite voir qu’il y a un seul résultat parmi les 12 résultats équiprobables possibles qui correspond à la sortie à la piscine avec Julie. La probabilité que Véronique se rende à la piscine avec Julie est donc égale à \(\frac{1}{12}\). Pour répondre aux deux autres questions, les élèves peuvent se référer aux 12 résultats possibles ou seulement à la roulette correspondant à la question. Ainsi, la probabilité que Véronique fasse une activité avec Fanny est égale à \(\frac{3}{12}\) ou \(\frac{1}{4}\). La probabilité qu’elle fasse du vélo est égale à \(\frac{4}{12}\) ou \(\frac{1}{3}\).
Après avoir déterminé ces probabilités, les élèves peuvent réaliser une expérience de probabilité pour vérifier la vraisemblance de leurs réponses en utilisant deux roulettes comme celles présentées ci-dessus. Les élèves peuvent aussi placer quatre jetons de couleur différente dans un premier sac et trois jetons de couleur différente dans un second sac. Chaque jeton du premier sac est associé à l’une des quatre amies, et chaque jeton du second sac est associé à l’une des trois activités. L’expérience consiste alors à piger un jeton de chaque sac et à noter les résultats. Le personnel enseignant doit rappeler aux élèves l’importance d’effectuer l’expérience un nombre suffisant de fois.
Note : Les situations impliquant des choix successifs font appel à la pensée combinatoire, une pensée qui est en émergence au cycle moyen. Il est donc recommandé de ne pas aller au-delà de deux choix successifs et de limiter le nombre de résultats possibles. Sinon, l’énumération de l’ensemble des résultats devient fastidieuse et il se peut que les élèves apprennent à traiter ces situations par obéissance plutôt que par logique.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 145-147.
ACTIVITÉ 2 : EXPÉRIENCE RÉPÉTÉE
Présenter aux élèves un sac contenant une bille rouge, une bille verte et une bille bleue. La situation consiste à piger, à deux reprises, une bille du sac et à noter sa couleur. Entre les deux tirages, la bille doit être remise dans le sac. Demander aux élèves de déterminer la probabilité d’obtenir :
- deux billes rouges;
- une bille rouge et une bille bleue;
- deux billes de couleur différente.
Cette situation s’apparente à la situation comprenant deux choix successifs présentée précédemment. La seule différence est que les deux choix comportent les mêmes possibilités de résultats. Pour résoudre le problème, les élèves doivent énumérer l’ensemble des neuf résultats équiprobables possibles. Pour ce faire, elles et ils peuvent utiliser :
• un diagramme en arbre;
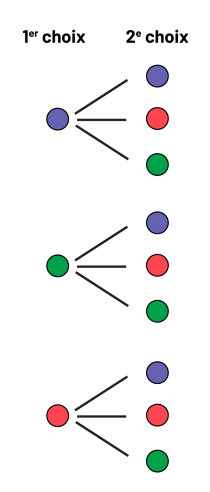 image Le
diagramme en arbre possède deux colonnes : premier choix et deuxième choix. Sous premier choix, trois jetons de
couleur sont placés l’un sous l’autre : un bleu, un vert et un rouge. Trois branches se déploient à partir de chacun
d’eux; elles présentent respectivement un jeton bleu, un jeton rouge et un jeton vert qui correspondent au deuxième
choix.
image Le
diagramme en arbre possède deux colonnes : premier choix et deuxième choix. Sous premier choix, trois jetons de
couleur sont placés l’un sous l’autre : un bleu, un vert et un rouge. Trois branches se déploient à partir de chacun
d’eux; elles présentent respectivement un jeton bleu, un jeton rouge et un jeton vert qui correspondent au deuxième
choix.
• un tableau;
| Bleue | Verte | Rouge | |
|---|---|---|---|
| Bleue | BB | BV | BR |
| Verte | VB | VV | VR |
| Rouge | RB | RV | RR |
• une liste ordonnée.
Bleue, bleue
Bleue, verte
Bleue, rouge
Verte, bleue
Verte, verte
Verte, rouge
Rouge, bleue
Rouge, verte
Rouge, rouge
À partir de ces résultats, les élèves peuvent déterminer que la probabilité d’obtenir :
- deux billes rouges est égale à \(\frac{1}{9}\);
- une bille rouge et une bille bleue est égale à \(\frac{2}{9}\);
- deux billes de couleur différente est égale à \(\frac{6}{9}\).
Les élèves devraient ensuite avoir l’occasion de vérifier la vraisemblance de leurs réponses en effectuant une expérience de probabilité.
Notons que, dans cette situation d’expérience répétée, le résultat de la seconde expérience ne dépend pas du résultat de la première. En mathématiques, on dit que ce sont des résultats indépendants. C’est là une autre occasion pour les élèves de comprendre l’idée que le hasard n’a pas de mémoire.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 147-149
ACTIVITÉ 3 : PROBABILITÉ THÉORIQUE
Dans ce qui suit, on présente le scénario pédagogique d’une situation de probabilité pour illustrer la façon d’amener les élèves à développer une meilleure compréhension des concepts liés à la probabilité théorique et à acquérir, par le fait même, une pensée probabiliste plus approfondie. Cette activité fait aussi ressortir une erreur que plusieurs personnes font lorsqu’il est question de probabilité, soit celle de ne pas tenir compte de tous les résultats possibles.
Le jeu des jetons bicolores
Former des équipes de trois élèves et remettre à chaque équipe deux jetons bicolores (par exemple, d’un côté vert et d’un côté rouge). Présenter ensuite la situation suivante :
Trois élèves décident de jouer à un jeu qui consiste à lancer en l’air deux jetons bicolores. Elles et ils
s’entendent au préalable sur ce qui suit : l’élève A gagne si le résultat des lancers correspond à deux côtés verts
( 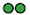 ), l’élève B gagne si le résultat correspond à
deux côtés rouges (
), l’élève B gagne si le résultat correspond à
deux côtés rouges (  ) et l’élève C gagne si le
résultat correspond à deux couleurs différentes (
) et l’élève C gagne si le
résultat correspond à deux couleurs différentes (  ). Selon vous, ce jeu est-il juste?
). Selon vous, ce jeu est-il juste?
Un jeu est juste si la probabilité de gagner pour chaque personne est la même.
1re étape : La prise de position
Demander d’abord à chaque élève d’indiquer aux autres membres de son équipe si elle ou il pense que le jeu est juste ou non, sans donner de raison.
Note : Le fait de demander aux élèves de prendre position dès le début de l’activité suscite leur intérêt et leur engagement. En effet, les élèves auront tendance ensuite à vouloir démontrer qu’elles et ils ont raison, et si ce n’est pas le cas, les élèves voudront comprendre pourquoi. De plus, puisque les élèves risquent de baser leur réponse sur une compréhension intuitive de la probabilité, le personnel enseignant pourra avoir une bonne idée de leur niveau de pensée probabiliste et pourra évaluer la mesure dans laquelle les fausses conceptions de la probabilité sont présentes.
Demander ensuite à chaque élève de justifier sa prise de position auprès des autres membres de son équipe. Par exemple, l’élève A pourrait affirmer que le jeu est juste puisqu’on a attribué à chaque élève un des trois résultats qu’il est possible d’obtenir à la suite du lancer des deux jetons bicolores, soit R, R; R, V et V, V. Les élèves doivent discuter des arguments présentés et tenter de s’entendre sur une prise de position commune pour l’équipe. Certaines et certains élèves pourraient être étonnés de voir que ce qu’elles et ils perçoivent comme étant une évidence peut être perçu différemment par les autres. Ces remises en question contribuent grandement à faire changer certaines des fausses conceptions en probabilité.
2e étape : L’expérience
Suggérer ensuite aux élèves d’effectuer une expérience afin de vérifier si la position retenue par leur équipe semble correcte. Chaque équipe doit lancer les deux jetons 10 fois, noter les résultats et les analyser pour voir si ces derniers confirment ou infirment leur position.
Préparer un tableau des résultats et demander à chaque équipe d’y inscrire leurs données. Voici un exemple de résultats possibles.
Résultats des lancers des jetons bicolores
| Équipe | Rouge, Rouge | Vert, Vert | Rouge, Vert |
|---|---|---|---|
| équipe 1 | 3 | 3 | 4 |
| équipe 2 | 5 | 0 | 5 |
| équipe 3 | 2 | 2 | 6 |
| équipe 4 | 3 | 2 | 5 |
| équipe 5 | 1 | 3 | 6 |
| équipe 6 | 3 | 4 | 3 |
| équipe 7 | 2 | 0 | 8 |
| équipe 8 | 1 | 2 | 7 |
| équipe 9 | 5 | 2 | 3 |
| équipe 10 | 2 | 4 | 4 |
Animer une discussion au sujet des résultats présentés dans le tableau en posant des questions telles que :
- Y a-t-il des équipes qui ont modifié leur position initiale, à savoir si le jeu est juste ou pas, à la suite des résultats obtenus? Si oui, pourquoi?
Note : Compte tenu du nombre restreint d’essais, il est fort possible que la position d’une équipe soit la bonne, mais que les résultats de l’expérience laissent croire le contraire.
- Que constatez-vous lorsque vous comparez les résultats obtenus par les différentes équipes? (Il y a une grande variabilité dans les résultats.)
- Selon les résultats, quelles équipes pourraient conclure que le jeu est juste? que le jeu n’est pas juste?
Discuter ensuite avec les élèves de la difficulté pour chaque équipe de tirer des conclusions à partir de seulement 10 essais. Afin d’augmenter la fiabilité des conclusions, suggérer aux élèves de considérer l’ensemble des résultats de toutes les équipes. En faisant la somme des résultats dans chaque colonne, on obtient le tableau qui suit.
Résultats des lancers des jetons bicolores
| Rouge, Rouge | Vert, Vert | Rouge, Vert | |
|---|---|---|---|
| Total des 100 essais | 27 | 22 | 51 |
Inciter les élèves à analyser ces données en posant des questions telles que :
- Que constatez-vous au sujet du nombre de résultats R, R et V, V? (Le nombre de résultats R, R est très semblable au nombre de résultats V, V.)
- Que constatez-vous au sujet du nombre de résultats R, V? (Il est nettement plus élevé que le nombre de résultats R, R et que le nombre de résultats V, V. En fait, il est presque équivalent à la somme des résultats R, R et V, V.)
- Qu’est-ce que ces données semblent indiquer au sujet du jeu? Pourquoi? (Les données semblent indiquer que le jeu n’est pas juste parce que l’élève C semble avoir une plus grande probabilité de gagner que les deux autres élèves.)
- Si on faisait 100 autres essais, est-il possible que les données nous portent à penser que le jeu est juste? (Si on tient compte de la variabilité des résultats obtenus par chacune des équipes, cela est en effet possible.)
3e étape : La théorie
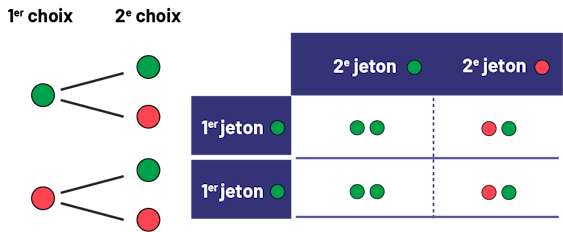
Souligner aux élèves qu’il serait important de trouver une autre façon de déterminer si le jeu est juste ou pas. Suggérer aux élèves d’analyser plus attentivement les résultats qu’il est possible d’obtenir à la suite du lancer de deux jetons bicolores. Pour faciliter cette analyse, écrire le nombre 1 sur les deux côtés du premier jeton et le nombre 2 sur les deux côtés du deuxième jeton. Expliquer ensuite que si on lance le premier jeton, deux résultats sont possibles, soit un côté vert ou un côté rouge et que ces deux résultats sont équiprobables. Puis, à la suite de chacun de ces deux résultats, on peut aussi obtenir un côté vert ou un côté rouge avec le lancer du deuxième jeton. Les résultats des lancers des deux jetons peuvent être représentés par le diagramme en arbre ou le tableau qui suivent.
 image
Diagramme en arbre. Premier choix : un jeton vert; deuxième choix : un jeton vert, un jeton rouge. Premier choix : un
jeton rouge; deuxième choix : un jeton vert, un jeton rouge. A droite la première rangée du tableau se nomme « Premier
jeton vert » et la deuxième rangée se nomme « Premier jeton rouge ». La première colonne se nomme « Deuxième jeton
vert » et la deuxième colonne se nomme « Deuxième jeton rouge ». Dans la case correspondant à premier jeton vert et
deuxième jeton vert, l’on trouve deux jetons verts. Dans la case correspondant à premier jeton vert et deuxième jeton
rouge, l’on trouve un jeton vert et un jeton rouge. Dans la case correspondant à premier jeton rouge et deuxième jeton
vert, l’on trouve un jeton rouge et un jeton vert. Et dans la case correspondant à premier jeton rouge et deuxième
jeton rouge, l’on trouve deux jetons rouges.
image
Diagramme en arbre. Premier choix : un jeton vert; deuxième choix : un jeton vert, un jeton rouge. Premier choix : un
jeton rouge; deuxième choix : un jeton vert, un jeton rouge. A droite la première rangée du tableau se nomme « Premier
jeton vert » et la deuxième rangée se nomme « Premier jeton rouge ». La première colonne se nomme « Deuxième jeton
vert » et la deuxième colonne se nomme « Deuxième jeton rouge ». Dans la case correspondant à premier jeton vert et
deuxième jeton vert, l’on trouve deux jetons verts. Dans la case correspondant à premier jeton vert et deuxième jeton
rouge, l’on trouve un jeton vert et un jeton rouge. Dans la case correspondant à premier jeton rouge et deuxième jeton
vert, l’on trouve un jeton rouge et un jeton vert. Et dans la case correspondant à premier jeton rouge et deuxième
jeton rouge, l’on trouve deux jetons rouges.
En examinant ces résultats, on constate qu’il y a une façon d’obtenir deux jetons verts, une façon d’obtenir deux jetons rouges et deux façons d’obtenir deux jetons de couleur différente. La probabilité d’obtenir deux jetons de couleur différente est donc plus grande que celle d’obtenir deux jetons rouges ou que celle d’obtenir deux jetons verts, ce qui confirme que le jeu proposé n’est pas juste.
On peut aussi observer qu’il y a deux façons d’obtenir deux jetons de couleurs différentes (V, R et R, V) et deux façons d’obtenir deux jetons de la même couleur (R, R et V, V). La probabilité d’obtenir deux couleurs différentes est donc égale à la probabilité d’obtenir la même couleur. Les résultats des 100 essais présentés dans le tableau plus haut illustrent assez bien ces probabilités (51 résultats R, V ou V, R et 49 résultats R, R ou V, V).
Demander aux élèves si les conclusions seraient différentes dans une situation où un même jeton bicolore est lancé à deux reprises. L’objectif est de les amener à reconnaître que les deux situations sont identiques, puisqu’il s’agit de résultats indépendants, c’est-à-dire que le résultat du lancer du deuxième jeton ne dépend pas du résultat du lancer du premier jeton. Il n’y a donc pas de différence, en ce qui a trait aux possibilités, entre deux lancers successifs d’un seul jeton ou d’un seul lancer de deux jetons.
Note : Plusieurs élèves ont de la difficulté à accepter que leur prise de position initiale ne soit pas correcte, même lorsqu’une explication théorique leur est fournie. Pour les aider, il est important de les exposer à une variété d’expériences de probabilité.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 151-155.
