D1.5 Déterminer la moyenne, la médiane et le ou les modes de divers ensembles de données représentées à l’aide de nombres naturels et de nombres décimaux, et expliquer ce que chacune de ces valeurs indique concernant les données.
HABILETÉ : EXPLIQUER CE QUE LES MESURES DE TENDANCE CENTRALE INDIQUENT CONCERNANT LES DONNÉES
Les mesures statistiques sont des nombres utilisés pour caractériser un ensemble de données. La moyenne, par exemple, est une mesure statistique. Les mesures statistiques sont présentées dans le cadre de la quatrième étape du processus d’enquête, soit l’interprétation des résultats, parce qu’elles constituent une autre façon d’attribuer un sens aux données et qu’elles peuvent fournir des renseignements sur lesquels il est possible de s’appuyer pour prendre une décision.
Différentes mesures statistiques sont couramment utilisées en traitement des données. Celles qui font l’objet d’étude au cycle moyen sont l’étendue, le mode, la médiane et la moyenne. Les élèves doivent bien comprendre ce que chacune représente afin de les choisir, de les déterminer et de les utiliser de façon appropriée.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 107.
CONNAISSANCE : MODE
Le mode d’un ensemble de données représente la ou les données ayant la plus grande fréquence, c’est-à-dire la ou les données qui paraissent le plus souvent. Le mode est particulièrement significatif dans des contextes d’enquêtes où il faut déterminer ce qui est le plus populaire, le plus vendu, le plus fréquent, etc. Comme en témoignent les exemples ci-dessous, il est possible de déterminer le mode d’un ensemble de données quantitatives ou qualitatives.
Exemple 1
Le tableau ci-dessous présente les données correspondant au nombre d’enfants dans les familles des élèves du groupe-classe. La donnée la plus fréquente est 2, ce qui indique qu’il y a davantage de familles de deux enfants. Le mode de cet ensemble de données quantitatives est donc deux enfants par famille.
Nombre d'enfants dans les familles des élèves de la classe
| Nombre d'enfants dans ta famille | Nombre d'élèves |
|---|---|
| 1 | 3 |
| 2 | 12 |
| 3 | 6 |
| 4 | 3 |
| plus de 4 | 2 |
Exemple 2
Le diagramme ci-dessous porte sur les couleurs préférées des élèves du groupe-classe. Pour déterminer le mode de ces données qualitatives, il suffit d’examiner la longueur des bandes. Or, la bande rouge et la bande bleue sont d’égale longueur et elles sont plus longues que toutes les autres. Dans ce cas-ci, il y a donc deux modes, soit le rouge et le bleu.
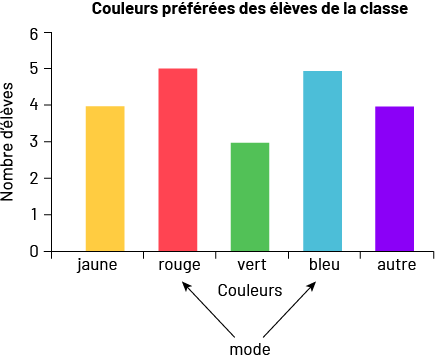 image Le diagramme
à 5 bandes colorées s’intitule : « Couleurs préférées des élèves de la classe ». L’axe horizontal se nomme « Couleurs
», tandis que l’axe vertical se nomme « Nombre d’élèves ». La bande jaune s’élève jusqu’au chiffre 4. La bande rouge
s’élève jusqu’au chiffre 5. La bande verte s’élève jusqu’au chiffre 3. La bande bleue s’élève jusqu’au chiffre 5, et
la bande violette qui signifie « Autres » s’élève jusqu’au chiffre 4. Avec des flèches, le mot « mode » pointe la
bande rouge et la bande bleue.
image Le diagramme
à 5 bandes colorées s’intitule : « Couleurs préférées des élèves de la classe ». L’axe horizontal se nomme « Couleurs
», tandis que l’axe vertical se nomme « Nombre d’élèves ». La bande jaune s’élève jusqu’au chiffre 4. La bande rouge
s’élève jusqu’au chiffre 5. La bande verte s’élève jusqu’au chiffre 3. La bande bleue s’élève jusqu’au chiffre 5, et
la bande violette qui signifie « Autres » s’élève jusqu’au chiffre 4. Avec des flèches, le mot « mode » pointe la
bande rouge et la bande bleue.
Exemple 3
Les données ci-dessous ont été enregistrées à l’occasion d’une compétition de saut en longueur.
- 1,04 m 1,06 m 1,12 m 1,13 m 1,16 m 1,19 m 1,22 m 1,28 m 1,36 m
Puisque toutes les données sont différentes, il n’y a pas de donnée ayant la plus grande fréquence. Cet ensemble de données n’a aucun mode. Cependant, les données pourraient être regroupées en catégories, comme dans le tableau ci-dessous. Dans un tel cas, le mode correspond à la catégorie ayant la plus grande fréquence, soit la catégorie de 1,10 m à 1,19 m.
Sauts en longueur
| Longueur (m) | Nombre d'élèves |
|---|---|
| 1,00 à 1,09 | 2 |
| 1,10 à 1,19 | 4 |
| 1,20 à 1,29 | 2 |
| 1,30 à 1,39 | 1 |
Lorsque le mode est utilisé pour répondre à une question d’intérêt ou prendre une décision, il est important de tenir compte de l’ensemble de données. En effet, dans certaines situations, la donnée la plus fréquente n’est pas nécessairement celle qui donne le meilleur sens aux données. Il est important d’inciter les élèves à examiner chaque situation de près avant de formuler des conclusions fondées sur le mode.
Voici quelques exemples de situations dans lesquelles est évaluée la pertinence d’utiliser le mode comme valeur représentative des données :
- Dans l’exemple 1 précédent, le mode deux enfants par famille semble assez représentatif de la situation puisqu’il y a un écart important entre cette fréquence et les autres.
- Dans l’exemple 2 précédent, non seulement y a-t-il deux modes (le rouge et le bleu), mais l’écart entre leur fréquence et les autres fréquences n’est pas très grand. Il est donc difficile de conclure que ces deux modes représentent une préférence de couleur marquée. Dans ce cas-ci, il serait préférable de mentionner que le rouge et le bleu sont légèrement plus populaires, mais que le jaune suit de près.
- D’après le diagramme à tiges et à feuilles ci-dessous, le mode correspond à 72 battements de cœur par minute. Ce nombre fait aussi partie de l’intervalle 70 à 79 qui compte le plus de données. Il représente donc bien cet ensemble de données.
| 6 | 3 5 5 8 9 |
| 7 | 1 1 2 2 2 2 2 4 5 7 7 |
| 8 | 2 3 6 |
| 9 | 1 2 |
| 10 | 8 |
- D’après la ligne de dénombrement ci-dessous, le mode correspond à 60 battements de cœur par minute. Ce nombre est éloigné de l’intervalle qui compte la plupart des données (69 à 77). De plus, l’étendue des données (29) est grande et les données ne paraissent qu’une, deux ou trois fois chacune. Il serait donc préférable de ne pas utiliser le mode pour formuler une conclusion au sujet de cet ensemble de données.
 image La ligne de
dénombrement s’intitule « Nombre de battements de cœur par minute des élèves de la classe ». Elle est graduée de 60 à
90. Avec une flèche, le mot « mode » pointe le nombre 60. Les nombres qui ne possèdent aucun X sont : 61, 63, 64, 65,
66, 68, 78, 79, 80, 82, 83, 84, 86, 87, 88, et 90. Les nombres 62, 67, 69, 70, 71, 74, 76, 77, 81, 85 et 89 possèdent
un X. Les nombres 72, 73 et 64 possèdent deux X. Le nombre 60 possède trois X.
image La ligne de
dénombrement s’intitule « Nombre de battements de cœur par minute des élèves de la classe ». Elle est graduée de 60 à
90. Avec une flèche, le mot « mode » pointe le nombre 60. Les nombres qui ne possèdent aucun X sont : 61, 63, 64, 65,
66, 68, 78, 79, 80, 82, 83, 84, 86, 87, 88, et 90. Les nombres 62, 67, 69, 70, 71, 74, 76, 77, 81, 85 et 89 possèdent
un X. Les nombres 72, 73 et 64 possèdent deux X. Le nombre 60 possède trois X.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 108-111.
CONNAISSANCE : MOYENNE
En mathématiques, la moyenne a un sens précis. Elle correspond à la valeur résultant d’un partage équitable; par exemple, si cinq amies et amis ont recueilli respectivement 5 $, 7 $, 7 $, 8 $ et 8 $ et qu’elles et ils mettent ces montants en commun pour les partager également, chacun recevra 7 $. La moyenne des montants recueillis est donc égale à 7 $. En mathématiques plus avancées, cette moyenne est appelée moyenne arithmétique. D’autres moyennes existent, comme la moyenne géométrique et la moyenne harmonique, mais elles ne sont pas à l’étude au cycle moyen. Le personnel enseignant devrait mettre l’accent sur la compréhension du concept de moyenne plutôt que sur la mémorisation de l’algorithme usuel (la somme des données divisée par le nombre de données). Pour ce faire, il devrait proposer aux élèves des activités qui font appel au modèle de partage équitable ou au modèle d’équilibre entre la somme des manques (différences entre la moyenne et les données qui sont inférieures à la moyenne) et la somme des surplus (différences entre la moyenne et les données qui sont supérieures à la moyenne). Autrement, les élèves n’acquièrent qu’une compréhension limitée du concept de moyenne.
Partage équitable
Les exemples ci-dessous montrent différentes situations qui font appel au modèle de partage équitable et qui contribuent à développer une bonne compréhension du concept de moyenne. Le modèle de partage peut être utilisé pour déterminer une moyenne sans avoir à recourir à l’algorithme usuel.
Exemple 1
Amir, Bruno, Carla, Denis et Elmira sont allés à la pêche et ont attrapé respectivement 2, 2, 3, 3 et 10 poissons. Détermine le nombre moyen de poissons pêchés.
Pour déterminer le nombre moyen de poissons pêchés, les élèves peuvent déterminer le nombre de poissons que
chaque personne aurait si les poissons étaient répartis également. Elles et ils peuvent d’abord illustrer la situation
initiale comme suit.
 image Titre de
l’exemple : Avant le partage. Des images de poissons rouges sont empilées au-dessus des noms de 5 élèves. Amir possède
deux poissons, Bruno possède deux poissons, Carla possède 3 poissons, Denis possède 3 poissons, et Elmira possède 10
poissons.
image Titre de
l’exemple : Avant le partage. Des images de poissons rouges sont empilées au-dessus des noms de 5 élèves. Amir possède
deux poissons, Bruno possède deux poissons, Carla possède 3 poissons, Denis possède 3 poissons, et Elmira possède 10
poissons.
Ensuite, les élèves font le partage : Elmira remet 2 poissons à Amir, 2 poissons à Bruno, 1 poisson à Carla et 1 poisson à Denis.

Après le partage, chaque personne a 4 poissons. Les élèves peuvent donc conclure qu’en moyenne, les 5 amies et amis ont pêché 4 poissons chacun.

Afin d’approfondir le concept de moyenne, il est important de donner l’occasion aux élèves de renverser le processus en leur demandant de créer un ensemble de données ayant une moyenne donnée. Cela renforce le concept de moyenne comme résultat d’un partage équitable.
Exemple 2
Six élèves d’un groupe-classe ont déterminé qu’elles et ils avaient, en moyenne, 5 stylos chacun. Quelle pourrait être une répartition possible des stylos parmi ces six élèves?
Puisque les 6 élèves ont en moyenne 5 stylos chacun, chaque élève aurait 5 stylos après le partage équitable.

Il y a donc un total de 30 stylos (6 x 5). Les 6 élèves peuvent alors répartir les 30 stylos entre elles et eux comme bon leur semble. Peu importe la répartition retenue, la moyenne de 5 stylos par élève sera maintenue. Voici un exemple d’une répartition possible :
 image Six colonnes
de stylos sont alignées côte à côte. La première colonne possède 5 stylos, la deuxième colonne possède 7 stylos, la
troisième colonne possède 4 stylos, la quatrième colonne possède trois stylos, la cinquième colonne possède 7 stylos
et la sixième colonne possède 4 stylos.
image Six colonnes
de stylos sont alignées côte à côte. La première colonne possède 5 stylos, la deuxième colonne possède 7 stylos, la
troisième colonne possède 4 stylos, la quatrième colonne possède trois stylos, la cinquième colonne possède 7 stylos
et la sixième colonne possède 4 stylos.
Il y a toujours un total de 30 stylos.
Une autre façon d’aider les élèves à développer une compréhension du concept de moyenne est de leur demander de déterminer une donnée manquante pour qu’un ensemble de données ait une moyenne particulière.
Exemple 3
Cinq élèves récoltent des fonds. Si les jeunes amassent en moyenne 25 $ chacune ou chacun, elles et ils gagnent des billets pour assister à un match de hockey. Lundi, 4 des 5 élèves se rencontrent et constatent qu’elles et ils ont récolté respectivement 29 $, 21 $, 31 $ et 13 $. Quelle est la somme d’argent minimale que Suzie, la 5e élève, doit avoir recueillie si le groupe veut gagner les billets de hockey?
Les élèves qui ont seulement appris à utiliser l’algorithme usuel pour déterminer la moyenne sont souvent incapables de répondre à ce genre de question. En effet, elles et ils ne sont pas en mesure d’adapter une recette apprise selon les circonstances, car elles et ils ne la comprennent pas. Les élèves qui ont développé une compréhension du concept de moyenne en tant que partage sont mieux équipées et équipés pour résoudre ce genre problème. Voici un échange que pourraient avoir les quatre élèves qui veulent déterminer la somme d’argent que Suzie doit avoir recueillie.
Élève 1 : Nous devons obtenir une moyenne de 25 $, ce qui veut dire que si nous partageons également l’argent entre nous, nous aurons 25 $ chacun. Moi j’ai amassé 29 $; je peux donc partager 4 $ avec vous.
Élève 2 : Moi je n’ai obtenu que 21 $; il me manque donc 4 $.
Élève 3 : Moi j’ai 6 $ de trop, car j’ai amassé 31 $.
Élève 4 : Je regrette. J’ai été malade en fin de semaine et j’ai seulement amassé 13 $. Il me manque 12 $.
Élève 1 : Utilisons l’idée du partage pour nous aider à déterminer la somme d’argent que Suzie doit avoir recueillie.
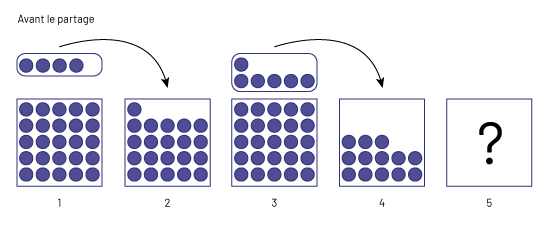 image Sous le titre
« Avant le partage », cinq boîtes sont alignées côte à côte. La première boîte contient 25 jetons. Au-dessus d’elle,
un ensemble de 4 jetons est lié à la deuxième boîte par une flèche. La deuxième boîte contient 21 jetons. La troisième
boîte contient 25 jetons, et au-dessus d’elle, un ensemble de 6 jetons pointe vers la quatrième avec une flèche. La
quatrième boîte contient 13 jetons. Quant à la cinquième boîte, elle ne contient pas de jetons, mais présente un point
d’interrogation.
image Sous le titre
« Avant le partage », cinq boîtes sont alignées côte à côte. La première boîte contient 25 jetons. Au-dessus d’elle,
un ensemble de 4 jetons est lié à la deuxième boîte par une flèche. La deuxième boîte contient 21 jetons. La troisième
boîte contient 25 jetons, et au-dessus d’elle, un ensemble de 6 jetons pointe vers la quatrième avec une flèche. La
quatrième boîte contient 13 jetons. Quant à la cinquième boîte, elle ne contient pas de jetons, mais présente un point
d’interrogation.
À la suite du partage, les trois premiers élèves ont chacun 25 $, mais il manque 6 $ au quatrième élève pour obtenir 25 $. Suzie doit donc apporter les 6 $ qui manquent en plus de ses 25 $. Elle doit donc avoir recueilli 31 $.
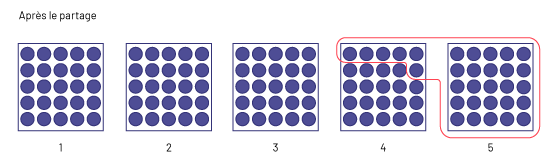 image Sous le titre
« Après le partage », cinq boîtes alignées côte à côte possèdent chacune 25 jetons. Par un tracé rouge, les 25 jetons
de la cinquième boîte et six jetons de la quatrième boîte sont regroupés pour former un ensemble.
image Sous le titre
« Après le partage », cinq boîtes alignées côte à côte possèdent chacune 25 jetons. Par un tracé rouge, les 25 jetons
de la cinquième boîte et six jetons de la quatrième boîte sont regroupés pour former un ensemble.
Équilibre entre la somme des surplus et la somme des manques
Le personnel enseignant peut aussi aider les élèves à développer une compréhension du concept de moyenne en leur présentant des situations qui font appel au modèle d’équilibre entre les surplus et les manques. Ce modèle, qui constitue en quelque sorte une variante du modèle de partage, est peut-être moins connu. Il est fondé sur l’idée que si, par exemple, un groupe d’élèves a un nombre moyen de jetons, certaines et certains élèves pourraient avoir moins de jetons que la moyenne alors que d’autres pourraient en avoir plus. Cependant, le total de ce que les élèves ont en moins doit être égal au total de ce que les élèves ont en plus. Les deux exemples ci-dessous illustrent cette idée.
Exemple 1
Cinq personnes ont 4 jetons chacune. Annie donne 1 jeton à Carl et 1 jeton à Daniel. Bahéya donne 1 jeton à Carl et 2 jetons à Eva.
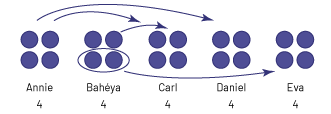 image Cinq
ensembles de 4 jetons bleus alignés côte à côte possèdent respectivement les noms suivants : Annie, Bahéya, Carl,
Daniel, Eva. Au-dessus du premier ensemble, des flèches pointent respectivement vers le troisième et le quatrième
ensemble. Au deuxième ensemble, une flèche pointe vers le troisième ensemble; deux jetons sont entourés et liés au
cinquième ensemble par une flèche.
image Cinq
ensembles de 4 jetons bleus alignés côte à côte possèdent respectivement les noms suivants : Annie, Bahéya, Carl,
Daniel, Eva. Au-dessus du premier ensemble, des flèches pointent respectivement vers le troisième et le quatrième
ensemble. Au deuxième ensemble, une flèche pointe vers le troisième ensemble; deux jetons sont entourés et liés au
cinquième ensemble par une flèche.
La moyenne est toujours de 4 jetons par personne. Or, par rapport à la moyenne, Annie a un manque de 2 jetons, Bahéya a un manque de 3 jetons, Carl a un surplus de 2 jetons, Daniel a un surplus de 1 jeton et Eva a un surplus de 2 jetons. Donc, par rapport à la moyenne, la somme des manques est de 5 jetons (2 + 3) et la somme des surplus est de 5 jetons (2 + 1 + 2). On constate que la somme des manques est égale à la somme des surplus. Si les surplus étaient distribués pour combler les manques, chaque personne aurait de nouveau 4 jetons.
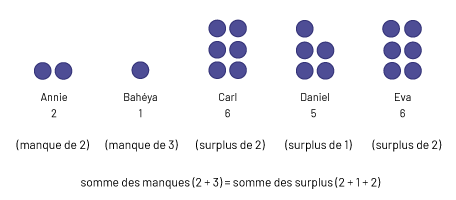 image Cinq
ensembles de jetons bleus alignés côte à côte possèdent respectivement les noms suivants : Annie, Bahéya, Carl,
Daniel, Eva. Le premier ensemble contient deux jetons et indique un manque de deux. Le deuxième ensemble contient un
jeton et indique un manque de trois. Le troisième ensemble contient 6 jetons et indique un surplus de deux. Le
quatrième ensemble contient cinq jetons et indique un surplus d’un. Et le cinquième ensemble contient 6 jetons et
indique un surplus de deux. Sous les ensembles apparait l’équation suivante : somme des manques parenthèse ouvrante
deux plus trois parenthèse fermante égale somme des surplus parenthèse ouvrante deux plus un plus deux parenthèse
fermante.
image Cinq
ensembles de jetons bleus alignés côte à côte possèdent respectivement les noms suivants : Annie, Bahéya, Carl,
Daniel, Eva. Le premier ensemble contient deux jetons et indique un manque de deux. Le deuxième ensemble contient un
jeton et indique un manque de trois. Le troisième ensemble contient 6 jetons et indique un surplus de deux. Le
quatrième ensemble contient cinq jetons et indique un surplus d’un. Et le cinquième ensemble contient 6 jetons et
indique un surplus de deux. Sous les ensembles apparait l’équation suivante : somme des manques parenthèse ouvrante
deux plus trois parenthèse fermante égale somme des surplus parenthèse ouvrante deux plus un plus deux parenthèse
fermante.
Le modèle d’équilibre entre les surplus et les manques peut être utilisé pour résoudre divers problèmes portant sur la moyenne. La situation ci-dessous présentée à l’Exemple 4 de la section Partage équitable et résolue à l’aide du modèle de partage, peut tout aussi bien être résolue à l’aide du modèle d’équilibre entre les surplus et les manques.
Exemple 2
Cinq élèves récoltent des fonds. Si les jeunes amassent en moyenne 25 $ chacune ou chacun, elles et ils gagnent des billets pour assister à un match de hockey. Lundi, 4 des 5 élèves se rencontrent et constatent qu’elles et ils ont récolté respectivement 29 $, 21 $, 31 $ et 13 $. Quelle est la somme d’argent minimale que Suzie, la 5e élève, doit avoir recueillie si le groupe veut gagner les billets de hockey?
Il faut d’abord examiner chaque somme d’argent par rapport à la moyenne de 25 $, puis déterminer le surplus ou le manque.
29 $ : surplus de 4 $
21 $ : manque de 4 $
31 $ : surplus de 6 $
13 $ : manque de 12 $
Ensuite, il faut déterminer la somme des surplus et la somme des manques.
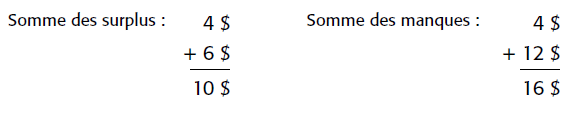
Ces deux sommes ne sont pas égales. Pour les équilibrer, il faut un surplus supplémentaire de 6 $ (16 $ – 10 $).
Suzie doit donc avoir recueilli 25 $ + 6 $, soit 31 $.
Lorsque les élèves ont acquis une bonne compréhension du concept de moyenne, elles et ils sont en mesure :
- de déterminer la moyenne d’un ensemble de données et de comprendre le lien entre les données et la moyenne;
- de créer un ensemble de données qui correspond à une moyenne particulière et de comprendre qu’une même moyenne peut provenir de plus d’un ensemble de données;
- de déterminer une donnée manquante d’un ensemble de données afin d’obtenir une moyenne particulière et de comprendre l’effet sur la moyenne de l’ajout de nouvelles données.
Ce n’est que lorsque cette compréhension est acquise que l’on devrait présenter aux élèves l’algorithme usuel pour calculer la moyenne, soit :

Soulignons que le fait de mettre l’accent sur la compréhension conceptuelle de la moyenne permet d’éviter certaines des erreurs conceptuelles ci-dessous qui ont été relevées par Konold et Higgins (2003, p. 203 et 204) :
- certaines et certains élèves prennent la moyenne pour le mode, c’est-à-dire qu’elles et ils l’associent à la valeur la plus fréquente;
- certaines et certains élèves associent la moyenne uniquement à un algorithme, ce qui fait qu’elles et ils ont de la difficulté à créer un ensemble de données qui correspond à une moyenne particulière;
- certaines et certains élèves prennent la moyenne pour la médiane, c’est-à-dire qu’elles et ils l’associent à la valeur au centre de l’ensemble de données.
Même lorsqu’une bonne compréhension des mesures statistiques est acquise, il n’est pas toujours facile, dans un contexte de prise de décision, de choisir la mesure qui correspond le mieux à une situation donnée. Au cycle moyen, il est donc préférable de s’en tenir à des situations simples.
Exemple 3
Mathieu veut négocier avec ses parents une augmentation du montant hebdomadaire d’argent de poche qu’ils lui donnent. En sachant qu’il ne peut pas simplement demander une augmentation sans motif valable, il décide d’effectuer un sondage auprès de ses camarades du cycle moyen afin de connaître le montant d’argent de poche qu’elles et ils reçoivent chaque semaine. Il organise les données recueillies sur une ligne de dénombrement.
 image La ligne de
dénombrement illustre avec des « X » des montants hebdomadaires d’argent de poche en dollars. À zéro, il y a quatre «
X ». À un, il y a un « X ». À un et demi, il y a deux « X ». À deux, il y a deux « X ». À deux et demi, il y a un « X
». À trois, il y a un « X ». À trois et demi, il y a quatre « X ». À quatre, il y a cinq « X ». À quatre et demi, il y
a quatre « X ». À cinq, il y a cinq « X ». À cinq et demi, il y a deux « X ». À six, il y a quatre « X ». À six et
demi, il n’y a aucun « X ». À sept, il y a un « X ». À sept et demi, il n’y a aucun « X ». À huit, il y a un « X ». À
8 et demi, 9 et 9 et demi, il n’y a aucun « X ». Et à dix, il y a six « X ».
image La ligne de
dénombrement illustre avec des « X » des montants hebdomadaires d’argent de poche en dollars. À zéro, il y a quatre «
X ». À un, il y a un « X ». À un et demi, il y a deux « X ». À deux, il y a deux « X ». À deux et demi, il y a un « X
». À trois, il y a un « X ». À trois et demi, il y a quatre « X ». À quatre, il y a cinq « X ». À quatre et demi, il y
a quatre « X ». À cinq, il y a cinq « X ». À cinq et demi, il y a deux « X ». À six, il y a quatre « X ». À six et
demi, il n’y a aucun « X ». À sept, il y a un « X ». À sept et demi, il n’y a aucun « X ». À huit, il y a un « X ». À
8 et demi, 9 et 9 et demi, il n’y a aucun « X ». Et à dix, il y a six « X ».
Mathieu analyse ensuite ces données afin de choisir une valeur sur laquelle il pourrait baser ses arguments en faveur d’une augmentation. Il constate que 10 $ est la valeur la plus fréquente. Il va voir son père et lui explique que, selon son sondage, il y a plus d’élèves du cycle moyen qui reçoivent 10 $ d’argent de poche que tout autre montant.
Son père trouve ce montant plutôt élevé et demande à voir l’ensemble de données. Après examen, il explique à Mathieu qu’en raison de la distribution des données le mode n’est pas la meilleure mesure pour représenter ces données. Puis, il détermine que la moyenne des montants alloués est de 4,66 $ et indique à Mathieu que ce montant semble plus approprié.
Un peu déçu, Mathieu calcule la médiane et constate qu’elle est de 4,50 $. Il comprend que dans cette situation, la moyenne et la médiane sont toutes deux de bonnes mesures pour représenter les données, mais comme la médiane est inférieure à la moyenne, il décide que ce n’est pas à son avantage de l’utiliser.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 115-125.
CONNAISSANCE : MÉDIANE
La médiane d’un ensemble de données correspond à la donnée qui se situe au centre de l’ensemble. Il y a donc le même nombre de données situées de part et d’autre de la médiane. Pour déterminer la médiane d’un nombre impair de données, il suffit de les mettre en ordre croissant ou décroissant et d’identifier la donnée qui se situe au centre. Dans le cas d’un nombre pair de données, la médiane correspond au nombre qui est à mi-chemin entre les deux nombres qui se situent au centre. Dans de tels cas, la médiane pourrait être un nombre qui ne fait pas partie de l’ensemble de données.
Exemple 1
Les données ci-dessous ont été enregistrées à l’occasion d’une compétition de saut en longueur.
1,04 m 1,06 m 1,12 m 1,13 m 1,16 m 1,19 m 1,22 m 1,28 m 1,36 m
Il y a 9 données, et elles sont mises en ordre croissant. La médiane de ces données est donc la cinquième donnée, soit 1,16 m. On remarque qu’il y a le même nombre de données (4) de chaque côté de la médiane.
Exemple 2
Le diagramme à tiges et à feuilles ci-dessous présente 22 données mises en ordre croissant. Deux données se situent au centre, soit la 11e et la 12e donnée. Il y a le même nombre de données (10) de chaque côté de ces deux nombres. Puisque ces deux données correspondent à 72 battements de cœur par minute, alors c’est la valeur attribuée à la médiane.
| 6 | 3 5 5 8 9 |
| 7 | 1 1 2 2 2 2 2 4 5 7 7 |
| 8 | 2 3 6 |
| 9 | 1 2 |
| 10 | 8 |
Exemple 3
Lors d’une campagne de financement pour leur équipe sportive, 10 élèves ont vendu des boîtes de chocolat. Voici le nombre de boîtes vendues :
15 12 11 10 10 8 7 6 5 5
La 5e et la 6e donnée se situent au centre de cet ensemble de 10 données mises en ordre décroissant. Ces deux données, soit 10 et 8, sont différentes. La médiane correspond alors au nombre 9, puisque 9 se situe à mi-chemin entre 8 et 10. Malgré le fait que cette médiane ne fasse pas partie de l’ensemble de données, on constate qu’il y a le même nombre de données, soit cinq, qui se situent de chaque côté d’elle.
Exemple 4
Voici les données relatives à la température quotidienne maximale, en degrés Celsius, dans une ville au mois de juin.
| Températures maximales en juin (°C) | ||||||
|---|---|---|---|---|---|---|
| 21 | 16 | 17 | 16 | 14 | 12 | 20 |
| 19 | 20 | 18 | 21 | 21 | 25 | 26 |
| 26 | 28 | 27 | 27 | 23 | 21 | 25 |
| 24 | 29 | 29 | 32 | 33 | 30 | 29 |
| 33 | 28 | |||||
Les élèves doivent d’abord mettre les nombres en ordre croissant. Pour ce faire, elles et ils peuvent les écrire dans un diagramme à tiges et à feuilles intermédiaire comme suit.
| 1 | 6 | 7 | 6 | 4 | 2 | 9 | 8 | ||||||||||||
| 2 | 1 | 0 | 0 | 1 | 1 | 5 | 6 | 6 | 8 | 7 | 7 | 3 | 1 | 5 | 4 | 9 | 9 | 9 | 8 |
| 3 | 2 | 3 | 0 | 3 |
Elles et ils peuvent ensuite replacer les feuilles dans chaque rangée en ordre croissant et obtenir le diagramme suivant.
| 1 | 2 | 4 | 6 | 6 | 7 | 8 | 9 | ||||||||||||
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 3 | 4 | 5 | 5 | 6 | 6 | 7 | 7 | 8 | 8 | 9 | 9 | 9 |
| 3 | 0 | 2 | 3 | 3 |
Afin d’aider les élèves à déterminer la médiane, le personnel enseignant peut leur suggérer d’écrire les nombres en ordre croissant sur une bande de papier et de la plier comme suit.
 image Les nombres
suivants sont écrits dans des cases placées l'une à la suite de l'autre : 12, 14, 16,16, 17, 18, 19, 20, 20, 21, 21,
21, 23, 24, 25, 26, 26, 27, 27, 28, 28, 29, 29, 29, 30, 32, 33, 33.
image Les nombres
suivants sont écrits dans des cases placées l'une à la suite de l'autre : 12, 14, 16,16, 17, 18, 19, 20, 20, 21, 21,
21, 23, 24, 25, 26, 26, 27, 27, 28, 28, 29, 29, 29, 30, 32, 33, 33.
L’utilisation de la bande de papier aide les élèves à développer une meilleure compréhension du concept de médiane. En pliant la bande en deux, les nombres sont associés deux à deux (le premier au dernier, le deuxième à l’avant-dernier, et ainsi de suite). Les élèves découvrent qu’il y a deux nombres au milieu, soit 24 et 25. De plus, elles et ils constatent qu’il n’y a aucun nombre entier entre 24 et 25. Elles et ils utilisent alors leurs connaissances des nombres décimaux pour déterminer que c’est le nombre 24,5 qui est situé à mi-chemin entre 24 et 25. La médiane de cet ensemble de données est donc 24,5 °C.
Exemple 5
Reprenons l’exemple 3 et ajoutons une variante comme suit :
Lors d’une campagne de financement pour leur équipe sportive, 10 élèves ont vendu des boîtes de chocolat. Voici le nombre de boîtes vendues.
15 12 11 10 10 8 7 6 5 5
Or, trois autres élèves n’ont pas encore indiqué le nombre de boîtes qu’elles et ils ont vendues. Si l’objectif était d’obtenir un nombre médian de 8 boîtes vendues, quel ensemble de données correspondant aux ventes des 13 élèves pourrait atteindre cet objectif?
Voici deux exemples de réponses possibles.
15 12 11 10 10 8 8 7 7 6 5 5 4
15 12 11 10 10 9 8 7 6 5 5 4 3
Si l’on ajoute, comme condition, que le mode de l’ensemble de données correspond aussi à 8 boîtes, les élèves
pourraient donner la réponse qui suit.
15 12 11 10 10 8 8 8 7 6 5 5 4
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 111-115.
