D1.4 Déterminer la moyenne et le ou les modes de divers ensembles de données représentées à l’aide de nombres naturels, et expliquer ce que chacune de ces valeurs indique au sujet des données.
Habileté : expliquer ce que la moyenne et le ou les modes indiquent au sujet des données
Les mesures statistiques sont des nombres utilisés pour caractériser un ensemble de données. Par exemple, la moyenne est une mesure statistique. Les mesures statistiques sont présentées dans le cadre de la quatrième étape du processus d’enquête, soit l’interprétation des résultats, parce qu’elles constituent une autre façon d’attribuer un sens aux données et qu’elles peuvent fournir des renseignements sur lesquels on peut s’appuyer pour prendre une décision.
Différentes mesures statistiques sont couramment utilisées en traitement des données. Les élèves doivent bien comprendre ce que chacune représente afin de les choisir, de les déterminer et de les utiliser de façon appropriée.
Source : adapté de Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 107.
Dans cette vidéo, les élèves déterminent le mode en ordonnant des tours de cubes emboîtables. Les élèves déterminent aussi la moyenne en redistribuant des cubes emboîtables dans les tours.
 Description de la vidéo
Description de la vidéo
Description à venir
CONNAISSANCE : MODE
Le mode d’un ensemble de données représente la ou les données ayant la plus grande fréquence, c’est-à-dire la ou les données qui paraissent le plus souvent. Le mode est particulièrement significatif dans des contextes d’enquêtes où on cherche à déterminer ce qui est le plus populaire, le plus vendu, le plus fréquent, etc. Comme en témoignent les exemples suivants, il est possible de déterminer le mode d’un ensemble de données quantitatives ou qualitatives.
Exemple 1
Le tableau ci-dessous présente les données correspondant au nombre d’enfants dans les familles des élèves de la classe. On constate que la donnée la plus fréquente est 2, ce qui indique qu’il y a davantage de familles de 2 enfants. Le mode de cet ensemble de données quantitatives est donc de 2 enfants par famille.
Nombre d'enfants dans les familles des élèves de la classe
| Nombre d'enfants dans ta famille | Nombres d'élèves |
|---|---|
| 1 | 3 |
| 2 | 12 |
| 3 | 6 |
| 4 | 3 |
| plus de 4 | 2 |
Exemple 2
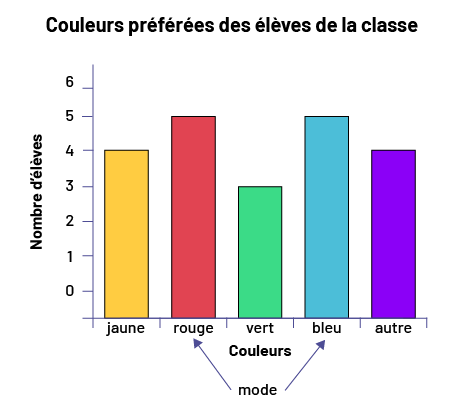
Le diagramme suivant porte sur les couleurs préférées des élèves de la classe. Pour déterminer le mode de ces données qualitatives, il suffit d’examiner la longueur des bandes. Or, on constate que la bande rouge et la bande bleue sont d’égale longueur et qu’elles sont plus longues que toutes les autres. Dans ce cas, il y a donc deux modes, soit le rouge et le bleu.
 Image
Le diagramme à 5 bandes colorées s’intitule : « Couleurs préférées des élèves de la classe ». L’axe horizontal se
nomme « Couleurs », tandis que l’axe vertical se nomme « Nombre d’élèves ». La bande jaune s’élève jusqu’au chiffre 4.
La bande rouge s’élève jusqu’au chiffre 5. La bande verte s’élève jusqu’au chiffre 3. La bande bleue s’élève jusqu’au
chiffre 5, et la bande pourpre qui signifie « Autres » s’élève jusqu’au chiffre 4. Avec des flèches, le mot « mode »
pointe la bande rouge et la bande bleue.
Image
Le diagramme à 5 bandes colorées s’intitule : « Couleurs préférées des élèves de la classe ». L’axe horizontal se
nomme « Couleurs », tandis que l’axe vertical se nomme « Nombre d’élèves ». La bande jaune s’élève jusqu’au chiffre 4.
La bande rouge s’élève jusqu’au chiffre 5. La bande verte s’élève jusqu’au chiffre 3. La bande bleue s’élève jusqu’au
chiffre 5, et la bande pourpre qui signifie « Autres » s’élève jusqu’au chiffre 4. Avec des flèches, le mot « mode »
pointe la bande rouge et la bande bleue.
Lorsqu’on utilise le mode pour répondre à une question d’intérêt ou pour prendre une décision, il est important de tenir compte de l’ensemble des données. En effet, dans certaines situations, la donnée la plus fréquente n’est pas nécessairement celle qui donne le meilleur sens aux données. Il est important d’inciter les élèves à examiner chaque situation de près avant de formuler des conclusions fondées sur le mode.
Voici quelques exemples de situations dans lesquelles on évalue la pertinence d’utiliser le mode comme valeur représentative des données :
- Dans l’exemple 1 précédent, le mode de 2 enfants par famille semble assez représentatif de la situation puisqu’il y a un écart important entre cette fréquence et les autres.
- Dans l’exemple 2 précédent, non seulement y a-t-il deux modes (le rouge et le bleu), mais l’écart entre leur fréquence et les autres fréquences n’est pas très grand. Il est donc difficile de conclure que ces deux modes représentent une préférence de couleur marquée. Dans ce cas, il serait préférable de mentionner que le rouge et le bleu sont légèrement plus populaires, mais que le jaune suit de près.
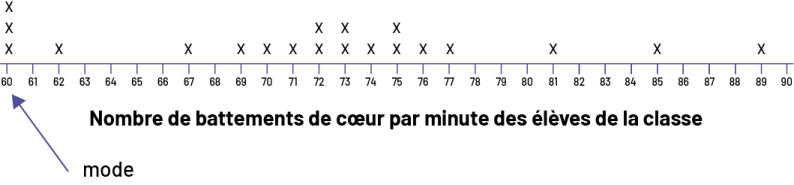
- D’après la ligne de dénombrement suivante, le mode correspond à 60 battements de cœur par minute. On constate que ce nombre est éloigné de l’intervalle qui compte la plupart des données (69 à 77). De plus, on voit que l’étendue des données (29) est grande et que les données ne paraissent qu’une, deux ou trois fois chacune. Il serait donc préférable de ne pas utiliser le mode pour formuler une conclusion au sujet de cet ensemble de données.
 Image
La ligne de dénombrement s’intitule « Nombre de battements de cœur par minute des élèves de la classe ». Elle est
graduée de 60 à 90. Avec une flèche, le mot « mode » pointe le nombre 60. Les nombres qui ne possèdent aucun X sont :
61, 63, 64, 65, 66, 68, 78, 79, 80, 82, 83, 84, 86, 87, 88, et 90. Les nombres 62, 67, 69, 70, 71, 74, 76, 77, 81, 85
et 89 possèdent un X. Les nombres 72, 73 et 64 possèdent deux X. Le nombre 60 possède trois X.
Image
La ligne de dénombrement s’intitule « Nombre de battements de cœur par minute des élèves de la classe ». Elle est
graduée de 60 à 90. Avec une flèche, le mot « mode » pointe le nombre 60. Les nombres qui ne possèdent aucun X sont :
61, 63, 64, 65, 66, 68, 78, 79, 80, 82, 83, 84, 86, 87, 88, et 90. Les nombres 62, 67, 69, 70, 71, 74, 76, 77, 81, 85
et 89 possèdent un X. Les nombres 72, 73 et 64 possèdent deux X. Le nombre 60 possède trois X.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 108-111.
CONNAISSANCE : MOYENNE
Selon le programme-cadre, le concept de moyenne est à l’étude pour la première fois en 3e année. Or, la plupart des élèves ont probablement déjà vu ou entendu les mots moyen ou moyenne dans les médias et au cours de leurs lectures (par exemple, la température moyenne, l’âge moyen, le cycle moyen). Il est alors important d’insister sur le fait que dans le langage courant, le mot moyenne peut avoir un sens général non défini. Par exemple, si on dit qu’en moyenne, un ou une élève devrait réussir 10 redressements en 30 secondes, on laisse entendre que c’est le nombre de redressements que la plupart des élèves devraient réussir, mais que certains élèves pourraient en réussir davantage et que d’autres pourraient en réussir moins.
En mathématiques par contre, la moyenne a un sens plus précis; elle correspond à la valeur résultant d’un partage équitable. Par exemple, si 5 amis ont recueilli respectivement 5 $, 7 $, 7 $, 8 $ et 8 $ et qu’ils mettent ces montants en commun pour les partager également, chacun recevra 7 $. La moyenne des montants recueillis est donc égale à 7 $. En mathématiques plus avancées, cette moyenne est appelée moyenne arithmétique. D’autres moyennes existent (par exemple, moyenne géométrique, moyenne harmonique), mais elles ne sont pas à l’étude au cycle moyen. Le personnel enseignant devrait mettre l’accent sur la compréhension du concept de moyenne plutôt que sur la mémorisation de l’algorithme usuel (la somme des données divisée par le nombre de données). Pour ce faire, il devrait proposer aux élèves des activités qui font appel au modèle de partage équitable. Autrement, les élèves n’acquièrent qu’une compréhension limitée du concept de moyenne.
Partage équitable
Les exemples suivants démontrent différentes situations qui font appel au modèle de partage équitable et qui contribuent à développer une bonne compréhension du concept de moyenne. Le modèle de partage peut être utilisé pour déterminer une moyenne sans avoir à recourir à l’algorithme usuel.
Exemple 1
Amir, Bruno, Carla, Denis et Elmira sont allés à la pêche et ont attrapé respectivement 2, 2, 3, 3 et 10 poissons. Déterminer le nombre moyen de poissons pêchés.
Pour déterminer le nombre moyen de poissons pêchés, les élèves peuvent déterminer combien de poissons chacun aurait si les poissons étaient répartis également. Ils peuvent d’abord illustrer la situation initiale comme suit.

Ensuite, ils procèdent au partage : Elmira remet 2 poissons à Amir, 2 poissons à Bruno, 1 poisson à Carla et 1 poisson à Denis.

Après le partage, chacun a 4 poissons. On peut donc conclure qu’en moyenne, les 5 amis ont pêché 4 poissons chacun.

Afin d’approfondir le concept de moyenne, il est important de donner l’occasion aux élèves de renverser le processus en leur demandant de créer un ensemble de données ayant une moyenne donnée. Cela renforce le concept de moyenne comme résultat d’un partage équitable.
Exemple 2
Six élèves d’une classe ont déterminé qu’ils avaient, en moyenne, 5 stylos chacun. Quelle pourrait être une répartition possible des stylos parmi ces six élèves?
Puisque les 6 élèves ont une moyenne de 5 stylos chacun, chaque élève aurait 5 stylos après le partage équitable.

Il y a donc un total de 30 stylos (6 x 5). Les 6 élèves peuvent alors répartir les 30 stylos entre eux comme bon leur semble. Peu importe la répartition retenue, la moyenne de 5 stylos par élève sera maintenue. Voici un exemple d’une répartition possible :

On peut vérifier qu’il y a toujours un total de 30 stylos.
On peut utiliser le modèle de partage pour développer une compréhension de l’algorithme usuel comme illustré dans l’exemple suivant. Le modèle donne en effet un sens à l’algorithme usuel puisqu’il démontre l’idée de regrouper les montants d’argent, puis de les partager parmi les amis (quotient de la somme des données par le nombre de données).
Exemple 3
Annie, Bahéya, Carl, Daniel et Eva ont respectivement 5 $, 6 $, 6 $, 8 $ et 10 $. Combien d’argent chacun a-t-il en moyenne?
On met d’abord les montants d’argent en commun pour constater qu’il y a 35 $ en tout. Cela correspond à l’opération 5 $ + 6 $ + 6 $ + 8 $ + 10 $ = 35 $. La somme est ensuite partagée équitablement et chacun reçoit 7 $, ce qui correspond à l’opération 35 $ ÷ 5 = 7 $.
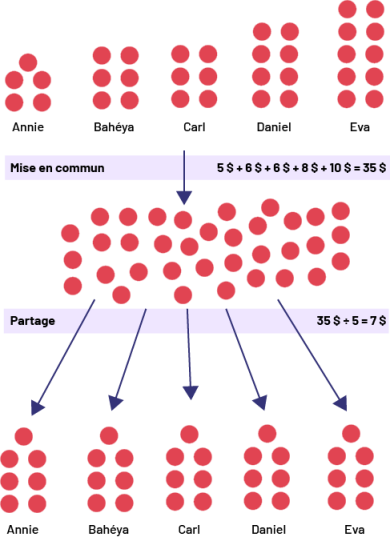 Image Dans
le haut de l’exemple 3, cinq noms d’élèves sont respectivement munis de quelques pastilles rouges. Annie possède 5
pastilles, Bahéya possède 6 pastilles, Carl possède 6 pastilles, Daniel possède 8 pastilles et Eva possède 10
pastilles. Sous les prénoms, il est écrit : Mise en commun, 5 dollars plus 6 dollars plus 6 dollars plus 8 dollars
plus dix dollars égale 35 dollars. Une flèche pointe vers le milieu de l’exemple 3 où toutes les pastilles sont mises
en commun pour un total de 35. Sous l’amas de 35 pastilles, il est écrit : Partage, 35 divisé par 5 égale 7 dollars.
Sous l’amas de 35 pastilles, 5 flèches pointent vers le bas sur chacun des prénoms qui sont répétés et où les
pastilles sont redistribuées équitablement. Annie, Bahéya, Carl, Daniel et Eva possèdent chacun 7 pastilles.
Image Dans
le haut de l’exemple 3, cinq noms d’élèves sont respectivement munis de quelques pastilles rouges. Annie possède 5
pastilles, Bahéya possède 6 pastilles, Carl possède 6 pastilles, Daniel possède 8 pastilles et Eva possède 10
pastilles. Sous les prénoms, il est écrit : Mise en commun, 5 dollars plus 6 dollars plus 6 dollars plus 8 dollars
plus dix dollars égale 35 dollars. Une flèche pointe vers le milieu de l’exemple 3 où toutes les pastilles sont mises
en commun pour un total de 35. Sous l’amas de 35 pastilles, il est écrit : Partage, 35 divisé par 5 égale 7 dollars.
Sous l’amas de 35 pastilles, 5 flèches pointent vers le bas sur chacun des prénoms qui sont répétés et où les
pastilles sont redistribuées équitablement. Annie, Bahéya, Carl, Daniel et Eva possèdent chacun 7 pastilles.
Le personnel enseignant peut profiter de cet exemple pour souligner aux élèves que la moyenne d’un ensemble de données n’est pas nécessairement un nombre qui fait partie de cet ensemble. Chez certains élèves, cette idée est difficile à comprendre.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 115-119.
