Fondements généraux du domaine Sens de l'espace
Cycle primaire
À cause de liens indissociables entre les deux anciens domaines Mesure et Géométrie et sens de l’espace, on trouve dans le programme-cadre de mathématiques 2020 ces deux domaines intégrés en un seul domaine, soit Sens de l’espace. La mesure et la géométrie sont des éléments de ce domaine développés dans les deux attentes E1 (Raisonnement géométrique et spatial) et E2 (Sens de la mesure).
Sens de l’espace
« Le sens de l’espace est la conscience intuitive que l’on a de son environnement et des objets qui s’y trouvent. »
(Ministère de l’Éducation de l’Ontario, 2005, p. 9).
Bien que le sens de l’espace sous-tende l’apprentissage de concepts géométriques, il joue aussi un rôle déterminant dans le développement du sens de la mesure. Selon Piaget (cité dans Lehrer, 2003, p. 180), la compréhension de la mesure entraîne une restructuration mentale de l’espace et englobe ainsi de plus en plus de subdivisions de l’espace. Ces subdivisions se traduisent par une quantité, une mesure.
Selon Clements (1999, p. 73), le sens de l’espace des enfants comme celui des adultes dépend de cartes mentales qui ne ressemblent en rien à la photo d’une carte papier ou électronique. Elles sont formées de connaissances ou de caractéristiques personnelles et comportent différentes idées ainsi que divers processus qui peuvent s’organiser selon des schèmes de référence variés. Plus l’enfant est jeune, plus les liens entre les représentations sont vagues. Ces représentations relèvent davantage de l’ordre spatial que visuel. Afin de faire preuve d’un sens de l’espace, les élèves doivent posséder des habiletés spatiales, notamment l’orientation spatiale et la visualisation. Grâce à l’orientation spatiale, elles et ils peuvent situer leur position par rapport à des objets ou à des points dans l’espace et peuvent se déplacer dans leur milieu. Les élèves comprennent et établissent des liens entre leurs différentes positions dans l’espace. Quant à la visualisation, elle leur permet de créer des images mentales, de les manipuler et de s’en servir pour faciliter la résolution de problèmes.
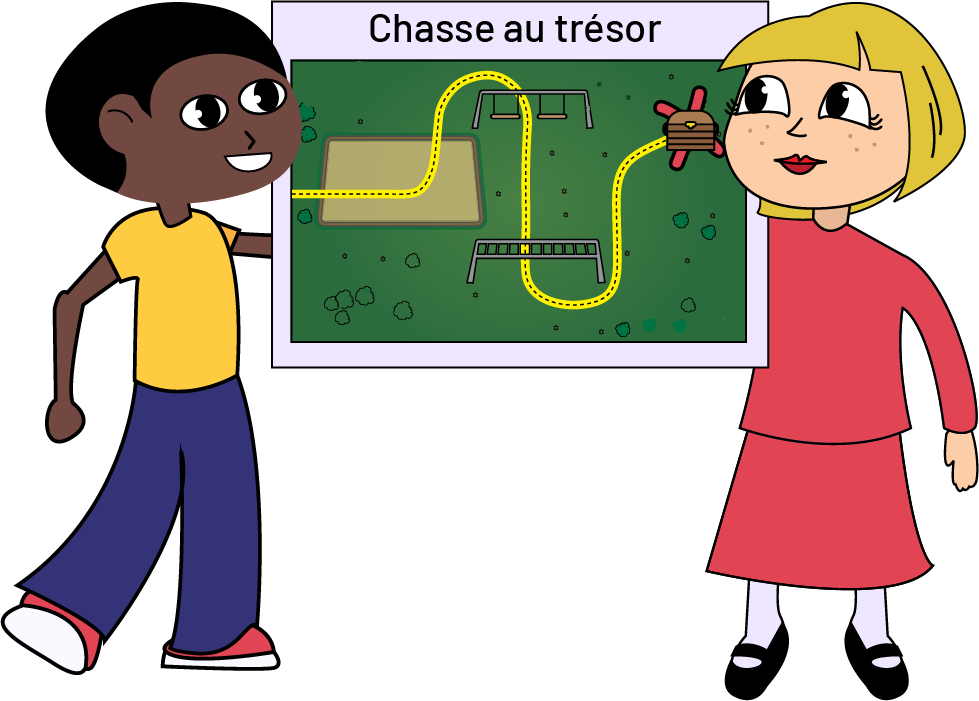
Le tableau ci-dessous résume la façon dont sont définies ces deux habiletés spatiales dans le contexte de la mesure et de la géométrie.
Habileté | Exemples |
Orientation spatiale Habileté à se situer ou à situer des objets dans son espace physique immédiat, et à effectuer ou à décrire des déplacements dans cet espace. |


|
Visualisation Habileté à se former et à décrire une représentation mentale de lieux, d’objets et de déplacements dans un espace bidimensionnel ou tridimensionnel. |
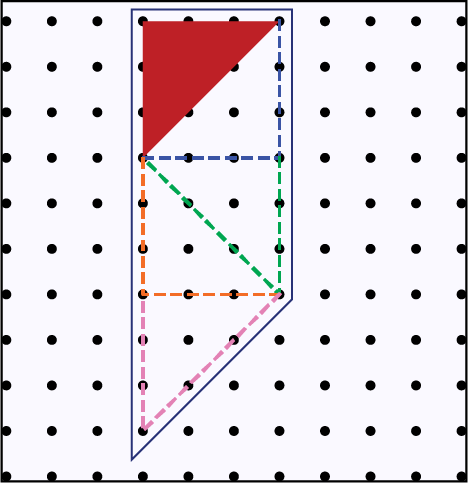
|
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 9-11.
Fondements en géométrie (attente E1)
« Qu’est-ce que la géométrie? La connaissance de la géométrie peut nous permettre d’apprécier davantage notre monde. On trouve des structures géométriques dans le système solaire, les formations géologiques, les cristaux, les plantes et même chez les animaux. La géométrie joue aussi un rôle majeur dans notre univers synthétique. L’art, l’architecture, les voitures, les machines, de fait presque tout ce que les humains créent comprend des formes géométriques. La géométrie est aussi utilisée quotidiennement par plusieurs personnes. À titre d’exemples, les scientifiques, les architectes, les artistes, les ingénieurs et les arpenteurs s’en servent régulièrement pour accomplir leur travail. Par ailleurs, notre connaissance de la géométrie nous est fort utile pour accomplir maintes tâches telles que dresser une clôture, construire une niche pour le chien, planifier le jardin, réaménager le salon. »
(Van de Walle, 2001, p. 308, traduction libre).
La géométrie, c’est :
- la science des figures de l’espace physique;
- l’étude des relations entre les points, les droites, les courbes, les surfaces et les volumes de l’espace réel;
- une connaissance intuitive des formes et des interrelations entre elles;
- un domaine d’études qui permet aux élèves de mettre en pratique un raisonnement spatial complexe afin de résoudre des problèmes dans tous les domaines des mathématiques et dans d’autres situations de la vie courante à l’école, à la maison, au jeu;
- une variété d’activités d’exploration avec des objets géométriques.
La géométrie, ce n’est pas :
- un savoir inné reçu à la naissance par quelques rares individus;
- un enseignement ou un apprentissage centré uniquement sur les règles, les procédures, le raisonnement analytique et les démonstrations;
- une mémorisation de définitions et de théorèmes;
- seulement une étude des figures planes et des solides.
Niveaux de pensée en géométrie
Depuis plusieurs années, des études dans le domaine de la géométrie ont eu une influence importante sur l’enseignement des concepts en géométrie. À la suite de recherches poussées, deux chercheurs hollandais, Dina Van Hiele-Geldof et Pierre Van Hiele, ont conçu un modèle du développement de la pensée géométrique. L’élément clé de ce modèle est une hiérarchie à cinq niveaux décrivant la compréhension des concepts en géométrie à différentes étapes du développement de la pensée de l’élève.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 2-3.
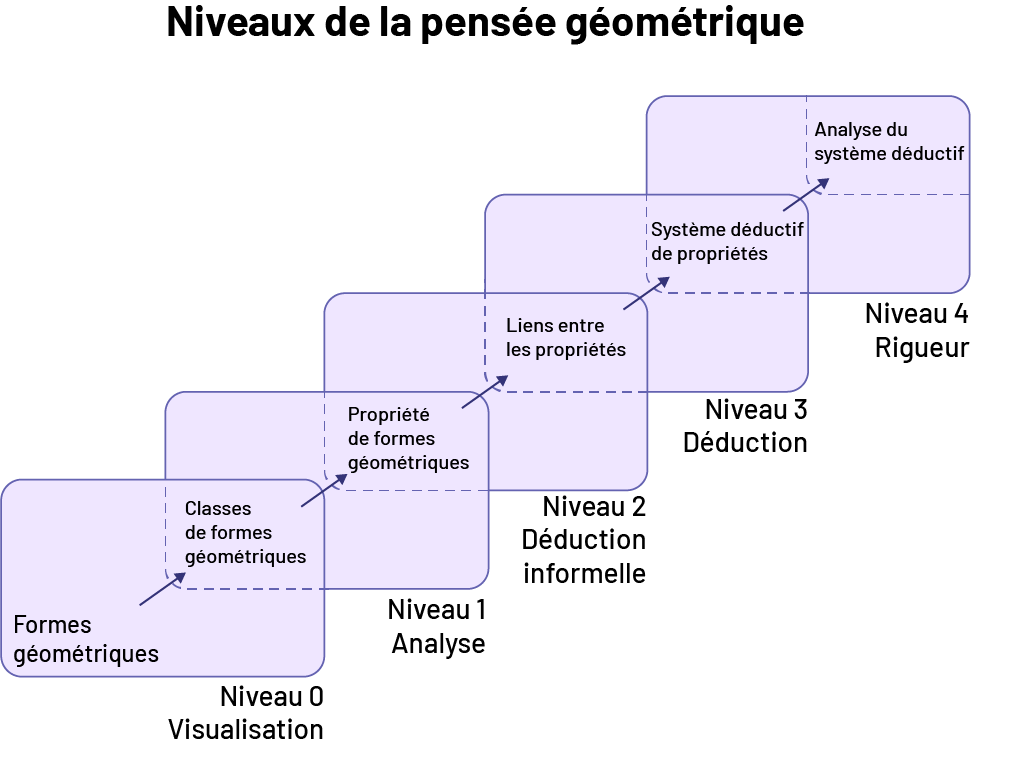 Niveaux de la pensée géométrique. Niveau zéro : visualisation. Niveau un : analyse. Niveau 2 : déduction informelle. Niveau 3 déduction. Niveau 4 : Rigueur. Chaque niveau est accompagné d’une carte avec une note. En partant du niveau zéro, formes géométriques, classes de formes géométriques, un, propriété de formes géométriques, 2, liens entre les propriétés, 3, système déductif de propriétés, 4, analyse du système déductif.
Niveaux de la pensée géométrique. Niveau zéro : visualisation. Niveau un : analyse. Niveau 2 : déduction informelle. Niveau 3 déduction. Niveau 4 : Rigueur. Chaque niveau est accompagné d’une carte avec une note. En partant du niveau zéro, formes géométriques, classes de formes géométriques, un, propriété de formes géométriques, 2, liens entre les propriétés, 3, système déductif de propriétés, 4, analyse du système déductif.Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 12.
Une brève description de ces cinq niveaux, ainsi que les comportements observables pour chacun, est présentée dans le tableau suivant.
DESCRIPTION | COMPORTEMENTS OBSERVABLES |
Niveau 0 – Visualisation | Niveau 0 – Visualisation |
Perception des figures géométriques selon leur apparence plutôt que leurs propriétés | L’élève :
Exemple d’énoncé : ✓ C’est un carré parce que ça ressemble à un carré, parce que je le vois, parce que c’est carré. |
Niveau 1 – Analyse | Niveau 1 – Analyse |
Début de l’analyse des formes géométriques pour en découvrir les propriétés | L’élève :
Exemple d’énoncé : ✓ Cette figure est un carré parce qu’elle a quatre sommets. ✓ Cette figure est un carré parce qu’elle a quatre coins droits. ✓ Cette figure est un carré parce qu’elle a quatre côtés égaux. ✓ Cette figure est un carré parce qu’elle a deux paires de côtés parallèles. |
Niveau 2 – Déduction informelle | Niveau 2 – Déduction informelle |
Établissement de liens ou de relations entre les propriétés d’une figure et entre les figures | L’élève :
Exemple d’énoncé : ✓ C’est un carré, mais c’est aussi un trapèze, car la propriété qui décrit le trapèze est qu’au moins deux côtés opposés sont parallèles. Je crois donc que le carré est une sorte de trapèze. ✓ Un carré est un rectangle, un parallélogramme et un quadrilatère parce qu’il possède toutes les propriétés de ces trois polygones. Un cube est aussi un prisme à base carrée ou un prisme à base rectangulaire. |
Niveau 3 – Déduction | Niveau 3 – Déduction |
Étude des définitions, des preuves, des théorèmes, des axiomes et des postulats | L’élève :
Exemple d’énoncé : ✓ Un parallélogramme qui a deux côtés adjacents de même longueur doit être un losange. |
Niveau 4 – Rigueur | Niveau 4 – Rigueur |
Étude de la géométrie de façon abstraite Note : Peu de recherches ont été faites sur ce niveau. | L’élève :
|
L’élève ne se situe pas nécessairement à un niveau particulier selon l’âge ou l’année d’études. De la 1re à la 5e année, selon les concepts présentés, elle ou il se situe généralement au niveau de la visualisation ou de l’analyse.
Elle ou il peut se situer au niveau de l’analyse par rapport à un concept et au niveau de la visualisation par rapport à un autre. Par exemple, l’élève décrit certaines propriétés du carré (niveau de l’analyse), mais ne reconnaît le parallélogramme que par son apparence (niveau de la visualisation).
Afin que l’élève passe d’un niveau à l’autre, elle ou il doit effectuer des expériences variées en géométrie qui doivent être accompagnées d’interventions pédagogiques efficaces de la part du personnel enseignant.
« Il faut des niveaux construits antérieurement pour atteindre un niveau plus élevé; ce qui est implicite dans un niveau devient explicite dans le niveau supérieur. [...] Chaque niveau présente un langage particulier où le sujet exprime un concept géométrique dans son propre langage avec l’utilisation de symboles et de relations. »
(Da Purifacação, 2000, p. 5).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 3-5.
Aperçu des grandes idées en géométrie
Les grandes idées sont présentées, explorées et développées afin d’aider le personnel enseignant à leur mise en œuvre dans ses stratégies d’enseignement et ses évaluations. Tout en étant interreliées, les grandes idées revêtent chacune une importance particulière.
Grande idée 1 : Interrelations
Des liens peuvent être établis entre les différents concepts en géométrie et sens de l’espace et le monde qui nous entoure.
Grande idée 2 : Propriétés des formes géométriques
Les formes géométriques et leurs propriétés permettent de décrire le monde qui nous entoure.
Grande idée 3 : Position et déplacement
La position et le déplacement des formes géométriques permettent de les situer dans le monde qui nous entoure.
La grande idée d’interrelations relie les deux autres grandes idées, puisque l’apprentissage de la géométrie et du sens de l’espace exige que l’élève établisse des liens avec le monde qui l’entoure.
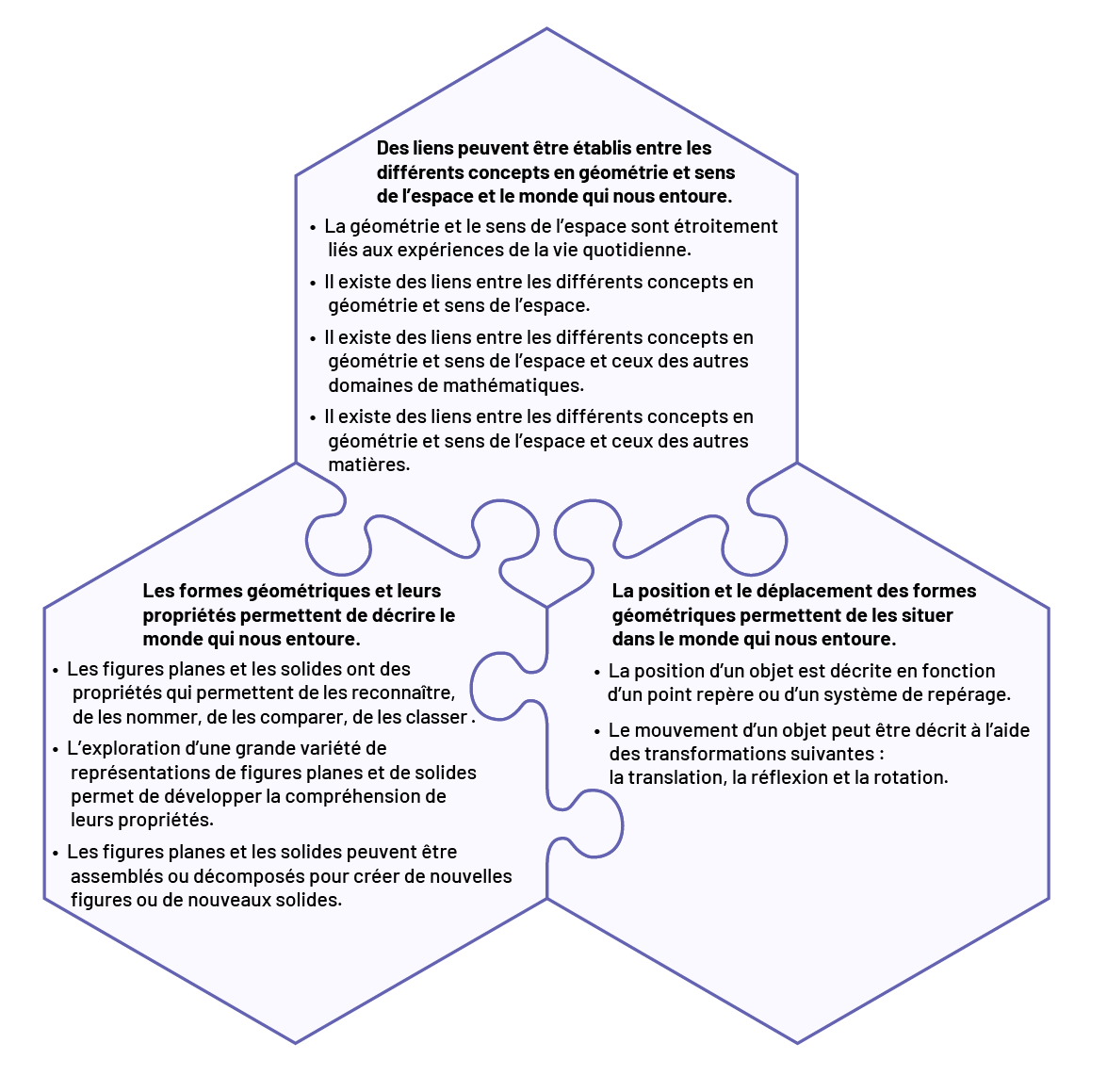 image 3 morceaux de casse-têtes sont imbriqués les uns avec les autres. Chaque morceau contient de l’information.Morceau un : des liens peuvent être établis entre les différents concepts en géométrie et sens de l’espace et le monde qui nous entoure.La géométrie et le sens de l’espace sont étroitement liés aux expériences de la vie quotidienne.Il existe des liens entre les différents concepts de géométrie et sens de l’espace.Il existe des liens entre les différents concepts en géométrie et le sens de l’espace et ceux des autres domaines en mathématique.Il existe des liens entre les différents concepts en géométrie et sens de l’espace et ceux des autres matières.Dans le deuxième morceau : La position et le déplacement des formes géométriques permettent de les situer dans le monde qui nous entoure.La position d’un objet est décrite en fonction d’un point repère ou d’un système de repérage.Le mouvement d’un objet peut être décrit à l’aide des transformations suivantes : la translation, la réflexion, la rotation.Le troisième morceau : Les formes géométriques et leurs propriétés permettent de décrire le mode qui nous entoure.Les figures planes et les solides ont des propriétés qui permettent de les reconnaître, de les nommer, de les comparer, de les classer.L’exploration d’une grande variété de représentations de figures planes et de solides permet de développer la compréhension de leurs propriétés.Les figures planes et les solides peuvent être assemblés ou décomposés pour créer de nouvelles figures ou de nouveaux solides.
image 3 morceaux de casse-têtes sont imbriqués les uns avec les autres. Chaque morceau contient de l’information.Morceau un : des liens peuvent être établis entre les différents concepts en géométrie et sens de l’espace et le monde qui nous entoure.La géométrie et le sens de l’espace sont étroitement liés aux expériences de la vie quotidienne.Il existe des liens entre les différents concepts de géométrie et sens de l’espace.Il existe des liens entre les différents concepts en géométrie et le sens de l’espace et ceux des autres domaines en mathématique.Il existe des liens entre les différents concepts en géométrie et sens de l’espace et ceux des autres matières.Dans le deuxième morceau : La position et le déplacement des formes géométriques permettent de les situer dans le monde qui nous entoure.La position d’un objet est décrite en fonction d’un point repère ou d’un système de repérage.Le mouvement d’un objet peut être décrit à l’aide des transformations suivantes : la translation, la réflexion, la rotation.Le troisième morceau : Les formes géométriques et leurs propriétés permettent de décrire le mode qui nous entoure.Les figures planes et les solides ont des propriétés qui permettent de les reconnaître, de les nommer, de les comparer, de les classer.L’exploration d’une grande variété de représentations de figures planes et de solides permet de développer la compréhension de leurs propriétés.Les figures planes et les solides peuvent être assemblés ou décomposés pour créer de nouvelles figures ou de nouveaux solides.Source : Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 9-10.
Fondements en mesure (attente E2)
« Si la mesure s’avère une partie intégrante de nos vies, nous prenons rarement conscience de la variété des mesures auxquelles nous recourons. Au cours d’une journée typique, nous utilisons très peu de mesures précises (par exemple, 350 ml de jus d’orange, 3 g de céréales, 20 l d’essence), mais nous estimons continuellement (par exemple, circuler environ à 50 km/h, faire un trajet d’environ une demi-heure, distribuer environ 25 feuilles). Nous utilisons fréquemment des unités de mesure non conventionnelles telles que trois boîtes de conserve, une pincée de sel, long comme six voitures. Nous recourons à plusieurs mesures comparatives ainsi qu’à des mesures moyennes. »
(Wilson et Rowland, 1993, p. 171, traduction libre).
La mesure jalonne nos activités et oriente, par le fait même, nos réflexions, nos décisions et notre perception du monde. Elle fait partie de nos activités quotidiennes à tel point que l’on en oublie la présence et l’importance. Ainsi, on se pose régulièrement des questions telles que « Qui en a plus que moi? », « À quelle distance est-ce? », « Quelle est la hauteur ou la longueur de cet objet? », sans nécessairement penser que l’on fait appel alors à une mesure. Dans toute situation, il est possible de mesurer les différentes caractéristiques d’un objet. Il importe donc de préciser la caractéristique, communément appelée attribut, qui fait l’objet d’une mesure.
Voici quelques exemples d’attributs mesurables que l’on peut quantifier par diverses unités de mesure non conventionnelles et conventionnelles.
acuité visuelle | intensité du son | taille |
aire | longueur | température |
angle | masse | temps |
capacité | périmètre | vitesse |
facteur de refroidissement | population | volume |
fréquence | profondeur | |
indice de rayons UV | superficie |
Attribut : caractère particulier d’un être, d’une chose.
La mesure est complexe et fait appel à des compétences qui vont au-delà de l’habileté à mesurer à l’aide d’un instrument de mesure tel qu’une règle ou une horloge. En effet, les élèves doivent reconnaître, comparer et estimer avec aisance les attributs mesurables d’un objet, les manipuler et les mesurer dans divers contextes afin que le vrai sens de la mesure puisse s’ancrer dans leurs expériences d’apprentissage, et qu’il les aide à résoudre divers problèmes de la vie courante ainsi qu’à prendre des décisions éclairées.
« Dès les premières années de scolarité, on présente d’abord la mesure comme une comparaison (par exemple, plus long que ou plus court que). Ensuite, au cours des années subséquentes, des concepts en mesure plus complexes se développent. Ces premiers concepts misent sur la compréhension des attributs longueur, aire et volume, et sur l’utilisation d’unités de mesure non conventionnelles pour mesurer et comparer. »
(Outhred, Mitchelmore, McPhail et Gould, 2003, p. 81, traduction libre).
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 5-7.
Sens de la mesure
« Quelques élèves peuvent visuellement segmenter des distances et utiliser des stratégies telles que « partie d’un tout » pour déterminer des longueurs manquantes. Elles et ils possèdent un « instrument de mesure interne ». Ce n’est pas une image statique; c’est plutôt un processus mental qui permet de se déplacer le long d’un objet, de le diviser et de compter les segments même sur des trajets très complexes, comme le périmètre de figures irrégulières. Ces élèves peuvent superposer cette « règle virtuelle » sur des objets et des formes géométriques (Steffe, 1991). Il s’agit du point critique dans leur développement du sens de la mesure. »
(Clements et Stephan, 2004, p. 306, traduction libre).
Chez quelques élèves, le sens de la mesure semble inné, comme s’il s’agit d’un talent légué à la naissance. Cependant, les recherches montrent que les élèves peuvent développer ce sens au moyen d’activités qui intègrent la manipulation de matériel concret et l’utilisation d’unités de mesure non conventionnelles et conventionnelles. Le développement du sens de la mesure dépasse l’apprentissage d’habiletés et de procédures relatives à l’acte de mesurer. Il constitue un cheminement structuré et organisé qui évolue et qui doit être adapté aux divers attributs mesurables d’un objet.
« Dans un sens, mesurer, c’est faire. Dans un autre, mesurer, c’est imaginer certains attributs de son milieu tels que la longueur et le temps. »
(Lehrer, 2003, p. 179, traduction libre).
Buys et de Moor (2005, p. 29) soulignent que le but premier de l’enseignement en mesure est de développer le sens de la mesure et que pour atteindre ce but, le personnel enseignant doit amener les élèves :
- à reconnaître les situations quotidiennes qui font appel à la mesure;
- à développer l’habileté à distinguer les différents attributs mesurables d’un objet et à déterminer les situations dans lesquelles les appliquer;
- à visualiser les diverses unités de mesure liées aux différents attributs;
- à employer correctement le vocabulaire relatif à la mesure.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 8.
« La mesure est souvent considérée comme la détermination de la grandeur, de la quantité ou le degré de quelque chose en utilisant un instrument gradué en unités conventionnelles. Une définition plus large de la mesure inclut la comparaison de cette chose avec un objet de grandeur connue, l’estimation de son étendue, sa qualité, sa valeur ou son effet et son évaluation fondée sur une comparaison avec une norme quelconque. »
(Dougherty et Venenciano, 2007, p. 452, traduction libre).
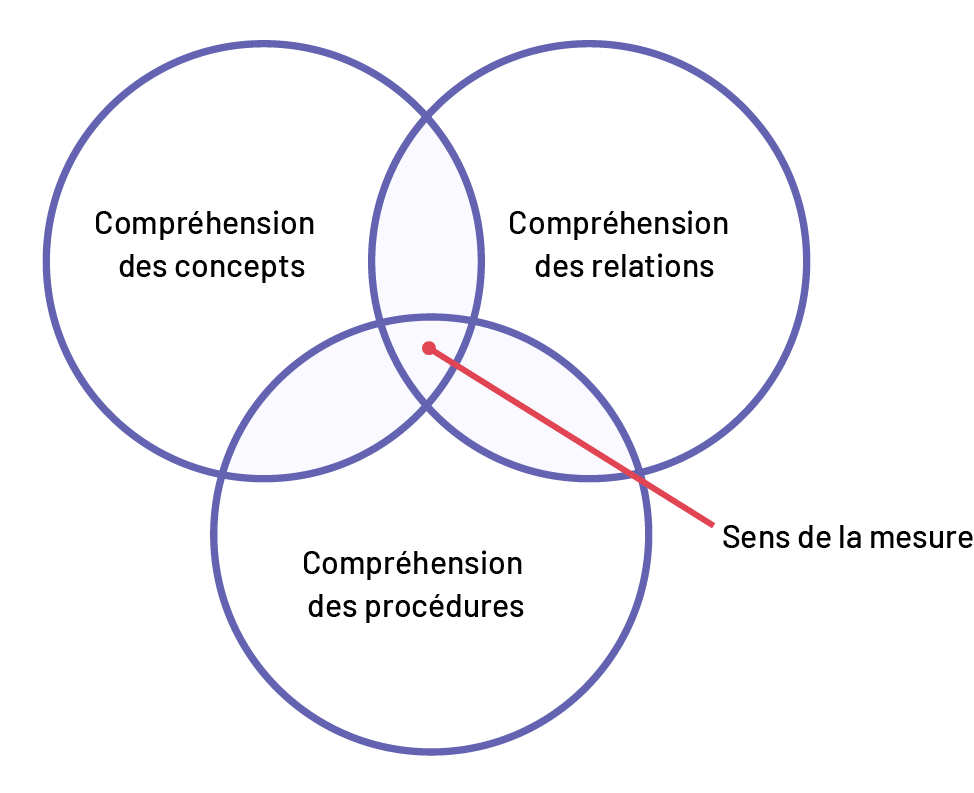
Le sens de la mesure, c’est construire les concepts relatifs à la mesure, établir des relations en mesure et savoir appliquer les procédures pour déterminer la mesure d’un objet.
Aperçu du Sens de la mesure
L’attente E2 et les contenus d’apprentissage relatifs à cette attente font appel à un grand nombre de concepts. Afin d’aider le personnel enseignant à planifier et à mettre en œuvre des stratégies qui offrent un enseignement efficace et cohérent, les concepts clés sont regroupés sous une seule grande idée, soit le sens de la mesure. Cette grande idée est présentée et développée en fonction de trois énoncés qui la sous-tendent : attributs et concepts fondamentaux, relations et acte de mesurer.
L’exploration de divers attributs, de relations ainsi que de procédures liées à l’acte de mesurer permet de développer le sens de la mesure.
Énoncé 1 – Attributs et concepts fondamentaux
La compréhension des attributs en mesure et des concepts fondamentaux qui les sous-tendent donne un sens aux unités de mesure et à l’acte de mesurer.
Énoncé 2 – Relations
La compréhension des diverses relations en mesure facilite la formulation de conjectures et de généralisations.
Énoncé 3 – Acte de mesurer
La compréhension des procédures nécessite de s’approprier toutes les étapes de l’acte de mesurer afin de consolider les concepts de mesure.
Au cycle primaire, les élèves développent leur sens de la mesure en explorant les attributs longueur, aire, capacité, masse et temps. Elles et ils utilisent la comparaison, la juxtaposition des unités de mesure et quelques instruments pour déterminer la mesure de ces attributs à l’aide d’unités de mesure non conventionnelles et d’unités de mesure conventionnelles de longueur et de temps. Les élèves explorent surtout la relation inverse et certaines relations entre les unités de mesure conventionnelles à l’étude.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 41-42.
Habileté à visualiser
« La visualisation consiste en l’habileté à percevoir, à transformer et à recréer différents aspects du monde spatial; elle met en jeu la capacité de penser au moyen de représentations visuelles et d’images mentales. »
(Armstrong, 1993, p. 10, traduction libre).
L’habileté à visualiser correspond à la capacité de se faire une image mentale d’une situation ou d’un concept abstrait. En mesure, cette habileté est liée principalement à la capacité de se faire une image mentale :
- de certains attributs mesurables;
- de repères associés aux divers attributs.
Visualiser certains attributs mesurables : La capacité de se faire une image de certains attributs mesurables aide les élèves à mieux en comprendre le sens. Au cycle primaire, les élèves doivent développer l’habileté à visualiser les attributs longueur, aire et capacité. En ce qui a trait aux attributs temps et masse, puisqu’ils ne représentent pas quelque chose qu’il est possible de voir ou d’illustrer, les élèves peuvent au mieux se faire une image mentale de quelques repères appropriés.
Pour l’attribut longueur, les élèves doivent visualiser un espace à une dimension, c’est-à-dire une image mentale d’une ligne droite ou d’une courbe. Par exemple, dans une situation où il est question de déterminer le périmètre d’une figure donnée, elles et ils doivent visualiser qu’il s’agit de déterminer la mesure de chacun des côtés qui correspond à la longueur de la ficelle placée autour de cette figure.
Les élèves doivent aussi reconnaître que, dans certaines situations, l’attribut longueur peut prendre un autre nom, par exemple :
- la hauteur d’une montagne;
- la largeur d’un prisme;
- l’épaisseur d’un gâteau;
- la taille d’une personne;
- la profondeur d’un lac;
- le périmètre d’une boîte.
Pour l’attribut aire, les élèves doivent visualiser un espace à deux dimensions, c’est-à-dire se faire une image mentale d’une surface plane ou courbe. Par exemple, dans une situation où il est question de déterminer l’aire d’un rectangle donné, elles et ils doivent visualiser qu’il s’agit de déterminer la mesure de l’espace occupé par la surface de cette figure.
Les élèves doivent aussi reconnaître que, dans certaines situations, l’attribut aire peut prendre un autre nom, par exemple :
- l’étendue d’un terrain;
- la superficie d’une ville.
Pour l’attribut capacité, les élèves doivent visualiser un espace à trois dimensions, c’est-à-dire se faire une image mentale de l’espace intérieur d’un contenant. Par exemple, dans une situation où il est question de déterminer la capacité d’un contenant, elles et ils doivent visualiser qu’il s’agit de déterminer la mesure de son espace intérieur. Au cycle intermédiaire, pour déterminer le volume, les élèves devront se faire une image mentale de l’espace qu’occupent les parois du contenant.

Visualiser des repères : La capacité de se faire une image mentale de certains repères associés aux attributs mesurables aide les élèves à estimer la grandeur d’un attribut ou à vérifier la vraisemblance d’un résultat obtenu à la suite de l’utilisation d’un instrument de mesure ou de l’application d’une formule. Par exemple, l’élève qui a retenu la règle à tableau comme repère pour représenter une mesure de 1 m peut se créer une image mentale de cette règle et l’utiliser pour estimer que la longueur d’un mur de la salle de classe mesure environ 4 m.

Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 20-22.
En géométrie, les élèves du cycle primaire étudient les propriétés des figures planes et des solides au moyen d’activités de construction (par exemple, construction avec un géoplan, des pailles, de la pâte à modeler, du carton, des cubes emboîtables) et de représentation sur papier (par exemple, représentation sur du papier quadrillé, du papier à points).
Ces activités aident les élèves à se construire une représentation mentale des figures planes et des solides fondée sur des propriétés précises et favorisent le développement d’habiletés liées à la visualisation.
Les activités de manipulation avec du matériel concret et de construction avec le géoplan sont particulièrement utiles à cet effet.
Pour les aider à développer l’habileté à passer d’un espace à l’autre et à consolider leurs connaissances des propriétés des solides, le personnel enseignant peut avoir recours à diverses activités de construction (par exemple, construire un modèle à l’aide de cubes, construire la coquille d’un solide à partir d’un développement donné) et à diverses activités de représentation (par exemple, tracer le développement d’un solide, associer un solide à son développement).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 28-29.
La visualisation spatiale est un type particulier de pensée spatiale qui implique l’utilisation de notre imagination pour « générer, mémoriser, extraire et transformer des images visuelles bien structurées » (Lohman, 1996, traduction libre, p. 98); elle est parfois considérée comme étant la capacité à penser avec l’« intelligence de l’œil ».
(Ministère de l’Éducation de l’Ontario, 2014, p. 10).
La visualisation spatiale se développe en mobilisant certaines habiletés spatiales qu’a énumérées John Del Grande (1990), y compris la rotation mentale.
| HABILETÉS SPATIALES RELATIVES À LA VISUALISATION SPATIALE | DESCRIPTION |
| 1. Coordination oculomotrice | Habileté à coordonner la vue et les mouvements du corps. |
| 2. Perception de plans (forme et fond) | Habileté à percevoir un élément précis figurant sur une toile de fond complexe (intersections, superpositions). |
| 3. Constance des formes | Habileté à reconnaître des figures géométriques indépendamment de leur taille, de leur couleur et de leur orientation dans l’espace. |
| 4. Perception des positions | Habileté à percevoir la position d’un objet par rapport à soi. Habileté à discriminer des objets identiques, peu importe leur orientation. |
| 5. Perception des relations spatiales | Habileté à percevoir la position d’au moins deux objets par rapport à soi ou d’un objet par rapport à l’autre. |
| 6. Discrimination visuelle | Habileté à remarquer les ressemblances et les différences entre deux ou plusieurs objets. |
| 7. Rotation mentale | Habileté à « […] faire tourner mentalement des objets bidimensionnels ou tridimensionnels » (Ministère de l’Éducation de l’Ontario, 2014, p. 13). |
(John Del Grande, 1990. © 2019, National Council of Teachers of Mathematics. The Arithmetic Teacher, vol. 37, no 6.)
Source : Guide d'enseignement efficace des mathématiques de la 7e à la 10e année, p. 12-13.
Habileté à résoudre une situation-problème
« Les élèves doivent résoudre des problèmes, non pour mettre en pratique les notions mathématiques qu’ils possèdent déjà, mais pour en apprendre de nouvelles. Lorsqu’ils doivent résoudre des problèmes judicieusement choisis et se concentrer sur les méthodes de solutions, il en résulte une nouvelle compréhension des concepts mathématiques intégrés dans la tâche. »
(Van de Walle et Lovin, 2007, p. 10).
L’habileté à résoudre des problèmes est un processus essentiel à l’apprentissage de la mesure. Afin d’aider les élèves à développer cette habileté, le personnel enseignant doit leur présenter divers types de situations-problèmes dont le contexte est signifiant. Il doit les inciter à faire appel à leurs connaissances antérieures ainsi qu’à leurs stratégies en résolution de problèmes, à communiquer clairement leurs résultats et à discuter des idées de leurs pairs lors d’échanges mathématiques. En étant ainsi engagées et engagés de manière optimale dans une réflexion portant sur les concepts visés, les élèves en clarifient le sens.
Les situations-problèmes en mesure doivent contribuer à améliorer la compréhension des élèves en ce qui a trait aux attributs et aux concepts fondamentaux, aux relations et à l’acte de mesurer. Il est essentiel que les élèves participent activement à la résolution de problèmes et aux discussions qui s’ensuivent. Ces expériences variées leur permettront de développer leur sens de la mesure.
Exemple
Les élèves doivent déterminer le plus long sentier entre deux sur une carte de piste cyclable. Le point de départ des deux sentiers est situé au même point sur la carte, à l’entrée du parc, et l’un d’entre eux se termine un peu plus loin que l’autre dans le parc. Elles et ils ont à leur disposition un bout de ficelle qui a été mesuré à l’avance pour être plus long que le tracé du plus long sentier. Les élèves doivent justifier leurs résultats par des arguments mathématiques et expliquer les méthodes employées pour procéder à la comparaison.
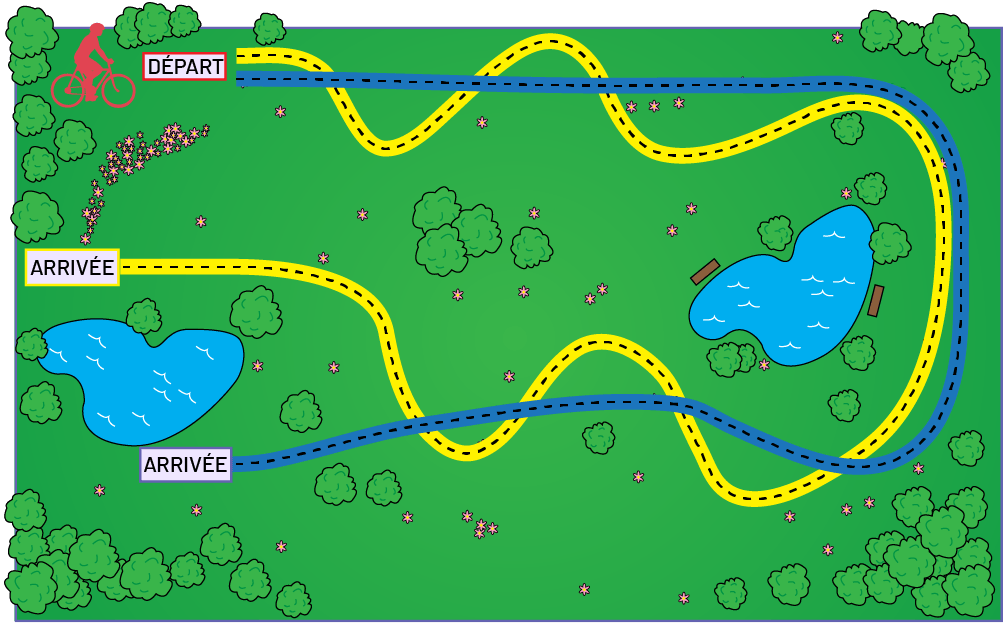
Lors d’un échange mathématique, l’enseignante ou l’enseignant invite les élèves à justifier leur réponse en posant des questions telles que :
- Quel est le plus long sentier? Comment le sais-tu? (J’ai regardé où commençait et où se terminait chacun des sentiers. J’ai vu que le point d’arrivée du sentier jaune était plus loin que celui du sentier bleu.)
- Est-ce que le fait que le point d’arrivée du sentier jaune soit plus loin que le point d’arrivée du sentier bleu nous permet de dire que le sentier jaune est plus long que le sentier bleu? Justifie ta réponse.
- Y a-t-il d’autres façons de déterminer le sentier qui est le plus long? (J’ai mesuré chacun des sentiers avec le bout de ficelle. La ficelle du sentier jaune était plus longue que celle du sentier bleu. J’aurais pu utiliser de la pâte à modeler, des cure-pipes ou encore de petits cubes emboîtables.)
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 22-23.
Habileté à raisonner
« Raisonner, c’est faire des inférences, généraliser et procéder à des validations. Les élèves font des inférences en déduisant l’information implicite de l’information donnée explicitement. »
(Small, 2005, p. 77, traduction libre).
Raisonner constitue un processus mental selon lequel des idées s’enchaînent de façon logique. Il s’agit d’une habileté importante puisqu’elle permet aux élèves de structurer leur pensée en intégrant un ensemble de connaissances et en établissant des relations entre elles. En mesure, les relations à établir sont nombreuses (par exemple, relations entre les attributs, relations entre les unités de mesure). L’habileté à raisonner dans un contexte de mesure permet aux élèves d’analyser les ressemblances et les différences entre les attributs mesurables, de tirer des conclusions et, ultimement, de réinvestir ces acquis dans un nouveau contexte ou dans une nouvelle situation. En leur demandant de justifier leur raisonnement et d’expliquer leurs démarches de résolution de situations-problèmes, le personnel enseignant profite de leur curiosité intellectuelle pour les amener à aller au-delà de la simple réponse et à réfléchir aux concepts fondamentaux propres à chaque attribut. Pour ce faire, il importe que le milieu d’apprentissage soit propice aux échanges mathématiques et fasse en sorte que les élèves se sentent à l’aise de formuler des conjectures et de les justifier.
Pour aider les élèves à acquérir l’habileté à raisonner en mesure, le personnel enseignant doit poser des questions ouvertes et proposer des situations-problèmes variées et complexes. Il doit les encourager :
- à représenter concrètement leur raisonnement en laissant des traces;
- à expliquer leur démarche et à justifier leurs résultats;
- à observer et à analyser les stratégies utilisées par les autres élèves.

Le carton a une longueur de 14 petits trombones. Si je mesure le carton avec de grands trombones, j’aurai besoin de moins de trombones.
Note : Le personnel enseignant a parfois tendance à demander aux élèves de justifier leur réponse seulement lorsque celle-ci est erronée. Par conséquent, lorsqu’on leur demande de justifier un résultat, les élèves ont tendance à penser qu’elles et ils ont commis une erreur. Il importe donc de les inciter régulièrement à justifier leur réponse, qu’elle soit correcte ou non. Ainsi, elles et ils saisiront qu’il s’agit là simplement d’une étape inhérente à tout raisonnement.
Le questionnement du personnel enseignant et les suggestions des pairs lors de l’échange mathématique peuvent aider les élèves :
- à réaliser qu’il est possible de résoudre la situation-problème donnée de façon plus simple;
- à formuler leur raisonnement;
- à émettre des conjectures et des généralisations plus complexes.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 24-25.
La nature du raisonnement mathématique des élèves est étroitement liée à leur capacité d’abstraction. Aux niveaux 0 et 1, les élèves utilisent surtout un raisonnement mathématique de type inductif, c’est-à-dire un raisonnement qui va du particulier au général. Ainsi, lorsqu’elles et ils manipulent un nombre limité de formes géométriques semblables et qu’elles et ils en observent les attributs ou les propriétés, elles et ils attribuent ces caractéristiques à l’ensemble des formes géométriques qui font partie de la même famille. Par exemple, après avoir manipulé un petit nombre d’objets de forme pyramidale, les élèves peuvent conclure que toutes les pyramides ont une extrémité pointue.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 36.
Habileté à communiquer
« En effet, c’est en examinant les stratégies et les idées proposées par d’autres que les élèves développent une pensée critique et parviennent à reconnaître et à dégager les forces et les limites d’un argument mathématique. Ce faisant, ils peuvent aussi apprécier la valeur du langage mathématique clair, juste et efficace. »
(Ministère de l’Éducation de l’Ontario, 2006, fascicule 2, p. 81).
Communiquer, c’est manifester sa pensée ou ses sentiments dans le but de se faire comprendre. Pour qu’il y ait communication, il est nécessaire d’avoir une intention, une situation, un contexte, un code, un message et une interaction explicite ou implicite entre des personnes.
L’habileté à communiquer en mesure se développe surtout dans un contexte de résolution de situations-problèmes ou d’un échange mathématique. Dans toute situation qui fait appel au raisonnement et à un argument mathématique, l’habileté à communiquer permet aux élèves de développer leur compréhension des concepts. La dimension sociale de la communication joue un rôle important dans l’acquisition de cette habileté et elle profite à toutes les personnes engagées dans l’acte de mesurer.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 26.
La capacité des élèves à présenter un argument mathématique reflète aussi leur niveau de pensée. Selon Radford et Demers (2004), les élèves du cycle primaire commencent à être capables de présenter un argument mathématique en utilisant des termes de causalité tels que alors, car ou parce que. Par contre, comme elles et ils n’ont pas toujours bien compris la notion de causalité, elles et ils utilisent parfois ces termes incorrectement pour justifier une conclusion ou la solution à un problème (par exemple, « C’est un carré parce que ça ressemble à un carré. »). Le personnel enseignant peut aider les élèves à développer l’habileté à utiliser les termes de causalité en leur donnant l’occasion de réagir de façon critique aux arguments présentés par d’autres élèves (par exemple, « Matéo dit que c’est un carré parce que ça ressemble à un carré. Selon vous, est-ce que c’est un argument clair et convaincant? »).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 37.
Au cycle primaire, la communication orale est un préalable à la communication écrite.
Communication orale
« Les jeunes enfants apprennent le langage par la communication orale. Il importe donc de leur fournir des occasions de “parler mathématiques”. L’interaction avec leurs pairs aide les élèves à acquérir des connaissances, à aborder différemment certaines notions et à clarifier leur propre pensée. »
(Rhone, 1995, p. 124, traduction libre).
La communication orale est la plus naturelle des formes d’expression utilisées par les élèves. La parole reste le moyen le plus utile et le plus fréquent de communiquer au quotidien. Elle est essentielle à la transmission d’idées, de découvertes, de démarches et de résultats en mesure. Elle sert de levier à la réflexion de l’élève et elle les engage dans un dialogue structuré qui les aide à donner du sens à leurs explorations. Afin d’aider les élèves à développer cette habileté, il faut leur fournir diverses occasions de s’exprimer et de montrer leur compréhension des différents concepts.
Au cycle primaire, lors des situations d’apprentissage en équipe et des échanges mathématiques, les élèves doivent apprendre à utiliser un vocabulaire relatif aux attributs et aux unités de mesure non conventionnelles. Elles et ils doivent comparer des objets entre eux en utilisant une terminologie appropriée et décrire la mesure à l’aide de termes justes et exacts.
Par exemple, en comparant leurs peluches, les enfants peuvent dire :
- Mon ourson est plus long que le tien;
- Le mien est plus court que le tien;
- Celui de Zoé est de la même hauteur que celui de Dylan.
Lorsque les élèves sont initiées et initiés aux mesures conventionnelles, elles et ils doivent non seulement comparer des objets à d’autres objets, mais en déterminer la mesure par des termes justes et exacts. Elles et ils diront par exemple : « Le périmètre du carré de sable est de 12 mètres et le périmètre de l’aire de jeu est de 24 mètres. »
Le personnel enseignant doit parfois guider les élèves dans l’utilisation d’un vocabulaire juste. Par exemple, si une ou un élève dit : « Mon morceau de gâteau est plus gros que le tien. », le personnel enseignant doit l’inviter à préciser sa pensée en lui demandant si son morceau de gâteau est plus long, plus épais ou plus large que celui de son amie.
Afin de promouvoir la communication entre les élèves, le personnel enseignant doit réduire la durée et la fréquence de ses interventions, et laisser la place aux échanges et aux analyses des idées émises par les équipes ou les individus. Avant de solliciter une réponse à une question, le personnel enseignant doit encourager les discussions de groupe et allouer un temps de réflexion suffisant.
« L’échange mathématique […] fournit à l’enseignante ou à l’enseignant des renseignements très utiles qui lui permettent d’évaluer le cheminement de l’élève et de planifier les prochaines étapes. Les conversations et les questions qui aident les élèves à développer leur vocabulaire aident aussi l’enseignante ou l’enseignant à analyser le degré de compréhension et les erreurs des élèves. »
(National Council of Teachers of Mathematics, 2000, p. 103, traduction libre).
Conjointement à la parole, les actions posées par les élèves peuvent contribuer à la communication en montrant la stratégie utilisée pour résoudre un problème ou pour la compréhension d’un concept en mesure.
Exemple 1
L’élève montre sa compréhension de l’aire en recouvrant la surface de mosaïques géométriques.

J’ai utilisé quatre losanges bleus, quatre triangles verts et un hexagone jaune pour couvrir le cerf-volant. Les formes ne se chevauchent pas.
Exemple 2
L’élève explique la façon dont elle a utilisé son soulier et son doigt pour mesurer la taille de son ami par itération.
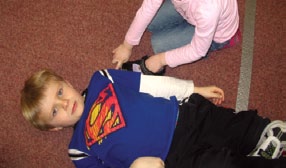
J’ai placé mon soulier à côté de mon ami. J’ai placé mon doigt au bout de mon soulier et après j’ai déplacé le soulier le long de mon ami à l’endroit où était mon doigt pour continuer à mesurer.
La communication écrite est un excellent moyen pour les élèves de clarifier leurs idées et de décrire leurs stratégies de résolution de problèmes. Par le fait même, elle constitue une bonne indication des apprentissages réalisés. En effet, les élèves révèlent souvent une part importante de ce qu’elles et ils ont appris et maîtrisé par les traces laissées sur leur feuille de travail. L’enseignante ou l’enseignant doit les encourager à laisser le plus de traces possibles.
Exemple 1
Au début de l’apprentissage, les élèves formulent souvent leur pensée mathématique par des dessins et des mots.

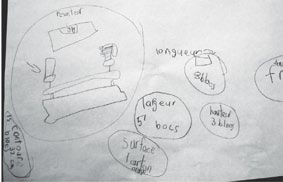
La communication écrite doit favoriser la représentation des outils utilisés pour résoudre les problèmes (par exemple, une disposition rectangulaire, une balance, un ruban gradué). Lorsque c’est possible, il faut permettre aux élèves d’utiliser le tableau interactif pour représenter leur solution. Celui-ci permet souvent une représentation plus juste et des traces plus exhaustives.
Pour aider les élèves à améliorer leurs solutions et leurs traces, le personnel enseignant doit encourager l’équipe à discuter de la tâche à accomplir, à anticiper des solutions possibles et à recourir à du matériel concret et des symboles familiers. Plusieurs outils favorisent l’amélioration de la communication écrite, par exemple, le mur de mots, les outils organisationnels, le journal mathématique, le tableau interactif.


En résumé, la communication écrite permet aux élèves :
- de consigner leurs apprentissages et de situer l’évolution de leur pensée mathématique dans un portfolio ou un journal mathématique;
- de prendre le temps de réfléchir et de s’organiser;
- de faire une objectivation relative à certains concepts;
- de profiter d’un espace d’expression personnel.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 26-31.
Le personnel enseignant demeure le soutien de l’actualisation du développement du Sens de l’espace en salle de classe. Son rôle ne se définit pas uniquement dans le choix des tâches, mais bien dans ses interventions qui visent à encourager les élèves à dépasser l’application des procédures afin qu’ils puissent développer une bonne compréhension conceptuelle des attributs en mesure et des propriétés géométriques ainsi que les concepts relatifs à la mesure et à la géométrie. Le personnel enseignant doit aussi les inciter à établir des liens entre les concepts, les relations et les procédures relatifs au Sens de l’espace.
Pour ce faire, le personnel enseignant doit :
- choisir des stratégies d’enseignement et d’apprentissage efficaces;
- choisir stratégiquement les pistes de questionnement;
- planifier et structurer l’échange mathématique;
- créer un milieu d’apprentissage propice au développement du sens de l’espace.
Choisir des stratégies d’enseignement et d’apprentissage efficaces : Une stratégie d’enseignement se définit comme une façon de faire, une approche, une série d’actions et de moyens que le personnel enseignant utilise dans un contexte donné. Un enseignement efficace en mesure ainsi qu’en géométrie amène les élèves :
- à réfléchir aux attributs et aux relations;
- à résoudre des problèmes de mesure tant dans des contextes de la vie courante que dans des contextes purement mathématiques;
- à faire preuve de motivation et d’engagement dans la résolution de ces problèmes;
- à discuter de leurs essais, des solutions possibles, de leur compréhension des concepts et des procédures.
Choisir stratégiquement les pistes de questionnement : Afin d’aider les élèves à développer une pensée mathématique qui reflète le sens de l’espace, le personnel enseignant doit s’assurer que les questions qu’il leur pose sont adaptées au moment, à la situation et à leur degré de compréhension. Pour ce faire, il doit choisir des questions qui aident entre autres les élèves à approfondir la compréhension des concepts, à établir des relations, à proposer des conjectures et à formuler des généralisations.
Planifier et structurer l’échange mathématique : Tout au long d’une situation d’apprentissage, le personnel enseignant planifie le déroulement de l’activité d’objectivation ou de l’échange mathématique. Pour ce faire, il observe attentivement les travaux des élèves et détermine, en fonction d’un ou de plusieurs objectifs, ceux qui devraient être présentés à l’ensemble de la classe. Ces travaux doivent susciter la discussion et aider les élèves à consolider leur compréhension des concepts visés.

La stratégie selon laquelle les travaux des élèves sont choisis et affichés dans la classe en fonction d’objectifs précis est parfois appelée stratégie du Bansho.
Ainsi, les travaux des élèves peuvent être choisis et affichés afin de mettre en évidence et de comparer :
- les stratégies de résolution de problèmes utilisées par les élèves (par exemple, illustrer la diversité des stratégies utilisées ou illustrer la même stratégie présentée selon différents niveaux de structure et d’organisation);
- le matériel utilisé par les élèves (par exemple, illustrer la différence entre une représentation faite à l’aide de dessins et une représentation faite à l’aide d’une règle, d’une disposition rectangulaire ou de symboles);
- la clarté de la solution proposée (par exemple, illustrer la différence entre une représentation partielle d’une solution et une représentation dans laquelle les élèves ont organisé, montré et expliqué leur solution clairement à l’aide de mots et de symboles).
Lors d’un échange mathématique, le personnel enseignant peut aussi décider d’exposer plusieurs travaux qui présentent des traces efficaces, mais différentes dans le but de permettre aux élèves d’observer plusieurs solutions possibles. Pendant l’échange mathématique, le personnel enseignant doit structurer l’échange en dirigeant les discussions et en effectuant des interventions stratégiques. Il doit s’assurer de clarifier les concepts visés et de faire en sorte que les élèves les comprennent bien. Au besoin, il peut terminer l’échange mathématique par le modelage d’une démarche, d’une stratégie ou d’une procédure efficace. Ce modelage peut être fait soit par le personnel enseignant, soit par une équipe d’élèves. Un échange mathématique bien structuré permet aux élèves de consolider leurs connaissances et leur compréhension des concepts et des procédures, et de reconnaître l’importance d’une communication efficace.
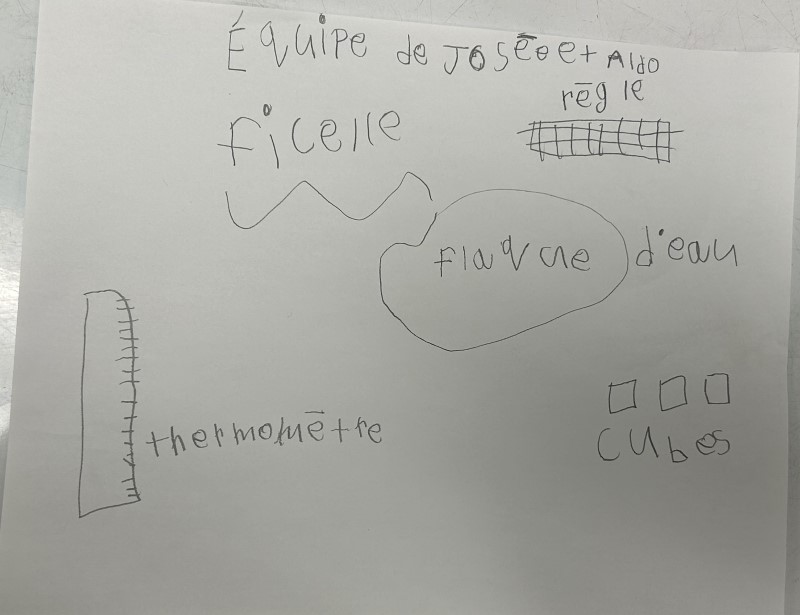

Note : L’ordre des présentations choisies permet de montrer deux stratégies différentes de représentations pour susciter la réflexion et la discussion des élèves. On peut constater que les traces laissées sur la représentation de droite sont plus détaillées et plus précises que celle de gauche. Les explications données permettent d’observer la progression de la compréhension du concept.
Créer un milieu d’apprentissage propice au développement du sens de l’espace : Un milieu d’apprentissage propice au sens de l'espace est un environnement où l’on mise autant sur le développement de la compréhension conceptuelle des propriétés géométriques, des attributs et des unités de mesure que sur la compréhension des procédures. Le personnel enseignant doit consciemment utiliser, tant en mathématiques que dans les autres matières, diverses situations qui font appel à la mesure et à la géométrie. C’est en étant régulièrement confrontées et confrontés au besoin de mesurer et d’effectuer des expériences variées en géométrie dans toutes sortes de situations que les élèves comprennent l’importance de la mesure et de la géométrie et qu’elles et ils développent les habiletés requises pour les obtenir.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 37-40.
