Fondements généraux du domaine Nombres
Cycle primaire
En élaborant un programme de mathématiques, il importe de se concentrer sur les principaux concepts mathématiques, ou « grandes idées », et sur les connaissances et les habiletés qui s’y rattachent.
Les grandes idées permettent au personnel enseignant d’avoir une vision globale des concepts à l’étude dans les différents domaines. Ce sont en quelque sorte des paramètres qui lui permettent :
- de prendre des décisions en ce qui a trait à l’enseignement (par exemple, de décider d’insister sur une leçon ou un ensemble de leçons);
- de déterminer les cotnnaissances antérieures des élèves;
- d’établir un lien entre la pensée et la compréhension de l’élève relativement aux concepts mathématiques à enseigner (par exemple, de prendre note des stratégies que l’élève utilise pour dénombrer);
- de recueillir des observations et de faire des rapports anecdotiques;
- de fournir une rétroaction aux élèves;
- de déterminer les prochaines étapes de l’apprentissage;
- de communiquer aux parents les concepts et une appréciation du rendement de leur enfant (par exemple, en inscrivant des commentaires dans le bulletin scolaire).
Il importe donc d’encourager le personnel enseignant à centrer son enseignement sur les grandes idées mathématiques. Le regroupement des attentes en fonction de quelques grandes idées permet de favoriser une compréhension plus approfondie des mathématiques.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 2-3.
Afin d’aider le personnel enseignant à se familiariser avec l’utilisation des « grandes idées » en mathématiques dans le cadre de leur enseignement et de leur évaluation, la présente section traite des cinq grandes idées qui constituent la base des attentes dans ce domaine au cours des premières années d’études, et des précisions sur les principaux concepts intégrés à chaque grande idée.
Grande idée 1 : dénombrement
Dénombrer requiert à la fois d’être capable de compter, de reconnaître les symboles et de comprendre les rapports entre les nombres et les quantités.
Grande idée 2 : sens des opérations
Saisir le sens des opérations exige de comprendre les concepts et les procédures qui entrent en jeu dans les opérations arithmétiques.
Grande idée 3 : quantité
Quantifier signifie associer un nombre à ce qui peut être dénombré ou mesuré.
Grande idée 4 : relations
Étudier les relations entre les nombres amène à reconnaître des régularités et à établir des liens importants.
Grande idée 5 : représentation
Représenter symboliquement un nombre suppose de saisir à la fois les concepts de chiffre, de quantité, de rang et de valeur de position.
Ces grandes idées, qui se recoupent, sont conceptuellement interdépendantes et également importantes. Par exemple, pour compter convenablement, il faut comprendre que le résultat du dénombrement représente une quantité. Le fait de pouvoir établir un lien entre cette connaissance et les relations qui caractérisent le système de numération en base dix permet aux élèves de disposer d’un fondement solide pour développer leur sens du nombre. Les trois grandes idées – dénombrement, quantité, relations – ont une incidence sur la grande idée sens des opérations, en ce qui concerne les actions des mathématiques. On trouve, dans les grandes idées, les représentations utilisées en mathématiques, soit les symboles des nombres, les algorithmes et les autres notations, telle la notation utilisée pour les nombres décimaux et les fractions.
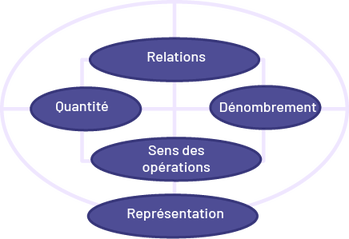 image Des mots ou expressions sont contenus dans des ovales bleus disposés sur un carré. Ils sont tous reliés entre eux par des lignes. En haut du carré, il y a le mot « Relations ». Au bas, il y a « Sens des opérations ». À gauche, il y a « Quantité ». Et à droite, il y a « Dénombrement ». Un grand ovale entoure l’ensemble. Au bas de cet ovale, il y a le mot « Représentation » contenu dans un ovale bleu.
image Des mots ou expressions sont contenus dans des ovales bleus disposés sur un carré. Ils sont tous reliés entre eux par des lignes. En haut du carré, il y a le mot « Relations ». Au bas, il y a « Sens des opérations ». À gauche, il y a « Quantité ». Et à droite, il y a « Dénombrement ». Un grand ovale entoure l’ensemble. Au bas de cet ovale, il y a le mot « Représentation » contenu dans un ovale bleu.Dans la section qui suit, on trouve, pour chacune des grandes idées du domaine Nombres, une description des énoncés qui la sous-tendent de la 1re à la 3e année.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 5-6.
Grande idée : Dénombrement
Aperçu et énoncés de la grande idée
Plusieurs des concepts mathématiques que les élèves acquièrent au cours des premières années d’études sont étroitement liés au dénombrement. L’habileté des élèves à dénombrer ainsi que la diversité et l’exactitude des stratégies de dénombrement utilisées sont de bons indicateurs de leur compréhension des mathématiques et de leurs progrès en la matière.

Les énoncés ci-dessous expliquent les points principaux à retenir au sujet du dénombrement dans les premières années d’études.
- Dénombrer suppose à la fois de réciter une série de nombres (compter) et de les associer à une série d’objets.
- Dénombrer implique d’être en mesure d’établir le lien entre une quantité et le nom ou le symbole du nombre qui la représente.
- Développer une compréhension conceptuelle du dénombrement a un lien direct avec la compréhension de la quantité, de la valeur de position et des opérations arithmétiques.
 image Des mots contenus dans des ovales bleus sont disposés en forme de losange et sont tous reliés entre eux par des flèches. En haut, il y a le mot « Compter ». Au centre, il y a « Dénombrer ». Au bas, il y a « Quantifier ». À gauche, il y a « Réciter ». Et à droite, il y a « Lire ».
image Des mots contenus dans des ovales bleus sont disposés en forme de losange et sont tous reliés entre eux par des flèches. En haut, il y a le mot « Compter ». Au centre, il y a « Dénombrer ». Au bas, il y a « Quantifier ». À gauche, il y a « Réciter ». Et à droite, il y a « Lire ».Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 9-10.
Grande idée : Quantité
Aperçu et énoncés de la grande idée
Les enfants découvrent la notion de quantité bien avant d’entrer à l’école. Les jeunes peuvent par exemple indiquer l’objet qui est plus gros ou plus petit qu’un autre, dire si deux quantités sont identiques ou si une quantité est plus grande qu’une autre. Même les tout-petits peuvent faire la différence entre un biscuit entier et la moitié d’un biscuit, et exprimer leur préférence. Toutefois, avoir un sens préliminaire de la quantité ne signifie pas pour autant être capable de compter. Avec le temps, les enfants font certains liens entre les mots utilisés pour compter et les quantités que ces mots représentent, mais ne comprennent pas nécessairement intuitivement la relation qui existe entre un nombre et la quantité qu’il représente.
Les énoncés ci-dessous expliquent les points principaux à retenir au sujet de la quantité dans les premières années d’études.
Quantifier signifie associer un nombre à ce qui peut être dénombré ou mesuré.
- Une quantité décrit un ordre de grandeur (le « nombre de » ou le « combien il y a de ») et constitue un concept essentiel au développement du sens du nombre.
- Il est important de saisir la notion de quantité pour comprendre le concept de valeur de position, les opérations arithmétiques et les fractions.
- Une compréhension du concept de quantité permet aux élèves d’effectuer des estimations et de jongler avec les nombres.
 image Des mots ou expressions contenus dans des ovales bleus sont disposés en forme de losange et sont tous reliés entre eux par des flèches. En haut, il y a le mot « Estimation ». Au centre, il y a « Quantité ». Au bas, il y a « Opérations ». À gauche, il y a « Valeur de position ». Et à droite, il y a « Nombre ».
image Des mots ou expressions contenus dans des ovales bleus sont disposés en forme de losange et sont tous reliés entre eux par des flèches. En haut, il y a le mot « Estimation ». Au centre, il y a « Quantité ». Au bas, il y a « Opérations ». À gauche, il y a « Valeur de position ». Et à droite, il y a « Nombre ».Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 43-44.
Grande idée : Relations
Aperçu et énoncés de la grande idée
Une bonne compréhension des relations qui existent entre les nombres permet aux élèves de faire des liens importants en mathématiques et constitue une base solide pour l’apprentissage des opérations arithmétiques de base et le développement du sens du nombre. Les élèves découvrent les relations en explorant les régularités trouvées dans diverses suites de nombres. Par exemple, dans la suite de nombres 2, 4, 6, 8, 10…, on observe que chaque nombre pair est 2 de plus que le précédent. Les élèves qui saisissent bien les relations entre les nombres de 1 à 10 peuvent faire plus facilement des transferts (par exemple, la différence entre 1 et 5 est la même qu’entre 21 et 25). Les élèves peuvent découvrir toutes sortes de relations entre les nombres en se servant d’une grille de nombres, d’une droite numérique ou d’un calendrier. L’habileté à reconnaître ces relations est importante tout au long du programme de mathématiques au palier élémentaire (par exemple, liens entre les opérations arithmétiques de base, liens entre les nombres rationnels et entre les nombres entiers négatifs).

Établir des relations entre les nombres signifie reconnaître et utiliser les régularités des nombres pour dégager des liens.
- Reconnaître et comprendre les régularités dans l’ensemble des nombres favorise l’établissement de liens entre ces nombres.
- Établir des liens entre les nombres permet de les comparer et de les ordonner pour mieux en saisir le sens.
- Explorer les relations entre les opérations arithmétiques de base permet de mieux les comprendre et les utiliser.
- Connaître les points d’ancrage 5 et 10 et leurs liens avec les autres nombres facilite la compréhension de la valeur de position et l’utilisation des opérations.
 image Des mots et expressions contenus dans des ovales bleus sont disposés en forme de losange et sont tous reliés entre eux par des flèches. En haut, il y a l'expression « Sens du nombre ». Au centre, il y a « Relations ». Au bas, il y a « Liens entre les opérations ». À gauche, il y a « Liens entre les nombres ». Et à droite, il y a « Régularités ».
image Des mots et expressions contenus dans des ovales bleus sont disposés en forme de losange et sont tous reliés entre eux par des flèches. En haut, il y a l'expression « Sens du nombre ». Au centre, il y a « Relations ». Au bas, il y a « Liens entre les opérations ». À gauche, il y a « Liens entre les nombres ». Et à droite, il y a « Régularités ».Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 59-60.
Grande idée : Représentation
Aperçu et énoncés de la grande idée
Le nombre est une représentation abstraite d’un concept très complexe. Les nombres sont le plus souvent représentés soit par une suite de symboles alphabétiques (par exemple, quinze), soit par une suite de symboles numériques (par exemple, 15). Ils sont utilisés dans divers contextes et c’est souvent le contexte qui précise le « sens » du nombre. Il suffit de penser, par exemple, aux différentes utilisations des nombres dans la phrase suivante : « Jean, qui est en 1re année, invite 15 enfants à son 7e anniversaire le 5 janvier 2004, à 14 h. » Comprendre le sens des différentes représentations et utilisations des nombres est fondamental au développement du sens du nombre.
Représenter symboliquement un nombre suppose de saisir à la fois les concepts de chiffre, de quantité, de rang et de valeur de position.
- L’habileté à représenter un nombre implique de savoir le lire et l’écrire en lettres et en chiffres, et pouvoir passer aisément d’une représentation à l’autre.
- La forme symbolique d’un nombre représente soit son nom, soit une quantité d’objets, soit un rang dans un ensemble ordonné. La valeur de chacun des chiffres qui composent le nombre dépend de la position qu’il occupe dans le nombre (par exemple, le chiffre 1 dans un nombre à trois chiffres peut signifier 1, 10 ou 100 selon sa position).
- L’habileté à saisir les liens qui existent entre la représentation symbolique des nombres (y compris les fractions et les nombres décimaux) et la quantité qu’ils évoquent est essentielle à l’acquisition du sens du nombre.
 image Des mots et expressions contenus dans des ovales bleus sont disposés en forme de losange et sont tous reliés entre eux par des flèches. En haut, il y a le mot « Chiffre ». Au centre, il y a « Représentation ». Au bas, il y a « Rang ». À gauche, il y a « Liens entre les nombres ». Et à droite, il y a « Valeurs de position ».
image Des mots et expressions contenus dans des ovales bleus sont disposés en forme de losange et sont tous reliés entre eux par des flèches. En haut, il y a le mot « Chiffre ». Au centre, il y a « Représentation ». Au bas, il y a « Rang ». À gauche, il y a « Liens entre les nombres ». Et à droite, il y a « Valeurs de position ».Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 71-72.
Grande idée : Sens des opérations
Aperçu et énoncés de la grande idée
Les élèves doivent comprendre les concepts et les procédures qui entrent en jeu dans les opérations arithmétiques. Une étude (Ma, 1999) sur les méthodes d’enseignement des opérations arithmétiques révèle que le personnel enseignant a tendance à mettre l’accent sur la dimension procédurale des opérations et à peu s’attarder aux concepts sous-jacents (par exemple, décomposition des nombres, valeur de position) ou aux liens qui existent entre les opérations (par exemple, la soustraction est l’opération inverse de l’addition).
En accordant davantage d’importance aux concepts sous-jacents, le personnel enseignant aide ses élèves à comprendre la façon dont les nombres et les opérations sont liés.
Pour acquérir ces concepts, les élèves doivent avoir de multiples occasions de représenter des situations de résolution de problèmes avec du matériel de manipulation, de créer leurs propres algorithmes et d’estimer le résultat d’additions, de soustractions, de multiplications et de divisions avant d’utiliser et de mémoriser les algorithmes usuels. Les énoncés ci-dessous expliquent les points principaux à retenir au sujet du sens des opérations dans les premières années d’études.

Saisir le sens des opérations exige de comprendre les concepts et les procédures qui entrent en jeu dans les opérations arithmétiques.
- L’habileté des élèves à développer et à utiliser des stratégies liées au dénombrement, à la valeur de position et à la décomposition leur permet d’effectuer les opérations arithmétiques avec efficacité.
- Les élèves prennent conscience des régularités dans des suites de nombres générées par les opérations arithmétiques en utilisant la droite numérique, la grille de nombres ou du matériel de manipulation.
- La compréhension des liens entre les opérations (par exemple, l’addition et la soustraction sont des opérations inverses) aide les élèves à apprendre les faits numériques de base et à résoudre des problèmes.
- Les élèves acquièrent le sens des opérations en développant et en utilisant des algorithmes dans des situations réelles de résolution de problèmes.
 image Des mots et expressions contenus dans des ovales bleus sont disposés en forme de losange et sont tous reliés entre eux par des flèches. En haut, il y a le mot « Régularités ». Au centre, il y a « Sens des opérations ». Au bas, il y a « Stratégies ». À gauche, il y a « Liens ». Et à droite, il y a « Algorithmes ».
image Des mots et expressions contenus dans des ovales bleus sont disposés en forme de losange et sont tous reliés entre eux par des flèches. En haut, il y a le mot « Régularités ». Au centre, il y a « Sens des opérations ». Au bas, il y a « Stratégies ». À gauche, il y a « Liens ». Et à droite, il y a « Algorithmes ».Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 25-26.
De nombreux principes d’enseignement s’appliquent à l’ensemble des premières années dans tous les domaines et soutiennent l’enseignement de toutes les grandes idées en mathématiques. Les plus importants sont repris en partie dans ce qui suit :
La communication orale entre les élèves est fondamentale pendant toutes les années d’études.
Les élèves ont besoin de parler des concepts mathématiques et de leur compréhension de ceux-ci, que ce soit avec d’autres élèves ou avec une ou un membre du personnel enseignant.
Diverses représentations de concepts favorisent la compréhension et la communication.
Les concepts peuvent être représentés de diverses façons (par exemple, à l’aide de matériel de manipulation, d’illustrations ou de symboles). L’élève qui utilise du matériel de manipulation ou des illustrations pour représenter un concept mathématique a plus de chances de le maîtriser. L’attitude de l’élève à l’égard des mathématiques s’améliore lorsque le personnel enseignant emploie efficacement le matériel de manipulation pour enseigner les concepts plus difficiles à saisir (Sowell, 1989; Thomson et Lambdin, 1994). Cependant, l’élève a besoin d’accompagnement dans son expérience des représentations concrètes et visuelles de manière à établir, d’une part, les liens appropriés entre le concept mathématique et, d’autre part, les symboles et le langage qui servent à le représenter.
La résolution de problèmes est un élément fondamental de l’apprentissage des mathématiques.
Les situations de résolution de problèmes offrent à l’élève des contextes intéressants et motivants, et lui permettent de comprendre la pertinence de cette discipline dans la vie quotidienne. Même les très jeunes enfants bénéficient de ce contexte d’apprentissage. Il est beaucoup plus valable pour les enfants d’apprendre les bases dans un contexte de résolution de problèmes pertinents et concrets que de mémoriser des procédures sans but précis.
Les élèves ont besoin d’effectuer de nombreuses expériences au moyen de ressources et de stratégies d’apprentissage diverses (par exemple, bandes numériques, droites numériques, grilles ou tapis de nombres, matériel de base dix, cubes emboîtables, cadres à dix cases, calculatrices, jeux mathématiques, chansons mathématiques, mouvements physiques, histoires de mathématiques).
Certaines stratégies (par exemple, le recours à des chansons mathématiques ou au mouvement) ne sont pas directement des activités de résolution de problèmes; néanmoins, elles sont utiles parce qu’elles répondent aux styles d’apprentissage de nombreux enfants, surtout dans les premières années d’études.
Devant des concepts d’une complexité croissante, il faut encourager l’élève à se servir de sa capacité de raisonnement.
Il importe que les mathématiques aient un sens pour l’élève et que l’élève ait les habiletés requises pour aborder les problèmes et les calculs mathématiques. Il faut l’encourager à appliquer sa capacité de raisonnement en l’aidant :
- à repérer des régularités : il convient de proposer aux élèves des expériences au cours desquelles on les amène à constater que le système de numération en base dix et les actions auxquelles on soumet les nombres (les opérations) sont fondées sur des régularités;
- à faire des estimations : l’élève qui apprend à faire des estimations peut déterminer si sa réponse est raisonnable. En apprenant à faire des estimations, l’élève dispose de points de repère ou de quantités connues (par exemple, « Voici ce à quoi ressemble un bocal de 10 cubes et un bocal de 50 cubes. Combien de cubes penses-tu qu’il y a dans celui-ci? »).
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 7-8.
En structurant les programmes en fonction des grandes idées et en mettant l’accent sur la résolution de problèmes, on offre aux élèves des situations d’apprentissage cohérentes qui leur permettent d’explorer les concepts en profondeur.
« Tout apprentissage, surtout un nouvel apprentissage, doit être intégré dans un contexte. Les contextes appropriés pour soutenir l’apprentissage sont ceux qui permettent aux élèves d’explorer et d’acquérir une compréhension initiale, de reconnaître et d’acquérir des compétences pertinentes, et d’élargir leur expérience en appliquant ces nouvelles connaissances. De tels environnements propices permettent aux élèves de “voirˮ les grandes idées en mathématiques ainsi que les principes sous-jacents, tels les modèles et les relations. » [traduction libre]
(Ontario Ministry of Education, 2005, p. 25)
Les enfants sont plus en mesure d’établir des liens en mathématiques et par conséquent d’apprendre les mathématiques si le programme est structuré de façon cohérente selon les grandes idées. Le regroupement des attentes en grandes idées facilite l’apprentissage des élèves et la formation professionnelle du personnel enseignant en mathématiques. Le personnel enseignant constatera qu’il est beaucoup plus utile de discuter et de déterminer les stratégies d’enseignement les plus efficaces pour une grande idée que d’essayer de déterminer les stratégies précises et les approches qui aideraient les élèves à réaliser des attentes particulières. Le recours aux grandes idées permet au personnel enseignant de comprendre que les concepts présentés dans le programme-cadre ne doivent pas être enseignés séparément, mais plutôt comme un ensemble de concepts interreliés. Pour élaborer un programme, le personnel enseignant doit avoir une connaissance approfondie des principaux concepts mathématiques de l’année d’études qu’il enseigne ainsi qu’une compréhension des liens entre ces concepts et l’apprentissage futur de ses élèves (Ma, 1999). Il doit notamment comprendre « la structure conceptuelle et les attitudes fondamentales inhérentes aux mathématiques à l’élémentaire » [traduction libre] (Ma, 1999, p. xxiv) ainsi que la meilleure manière d’enseigner ces concepts aux enfants. Le développement de ces connaissances permet de rendre l’enseignement plus efficace.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 2-3.
« La communication, entendue comme activité sociale et culturelle médiatisée par la langue, les symboles scientifiques et les outils technologiques, apparaît comme l’un des moyens privilégiés d’appropriation du savoir. En participant à une discussion avec ses pairs et le personnel enseignant, l’élève acquiert une conscience de plus en plus nette des objets d’apprentissage. » (Citation adaptée de Radford et de Demers, 2004, p. 15, traduction libre)
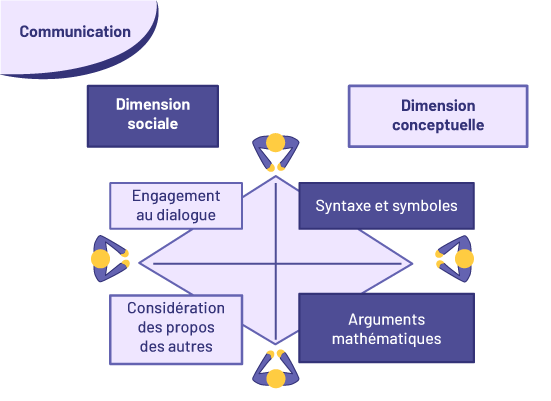 image Une table en forme de losange est vue d’en haut, il y a une personne assise à chacun des coins. Toutes les personnes sont reliées entre elles par une ligne. Le schéma s’intitule « Communication ». À gauche de la table, il est écrit « Dimension sociale » dans un rectangle bleu, et à droite de la table, il est écrit « Dimension conceptuelle » dans un rectangle violet. Entre les personnes assises au nord et à l’ouest, il est écrit « Enseignement au dialogue » dans un rectangle violet. Entre les personnes assises à l’ouest et au sud, il est écrit « Considération des propos des autres » dans un rectangle violet. Entre les personnes assises au nord et à l’est, il est écrit « Syntaxe et symboles » dans un rectangle bleu. Et entre les personnes assises à l’est et au sud, il est écrit « Arguments mathématiques » dans un rectangle bleu.
image Une table en forme de losange est vue d’en haut, il y a une personne assise à chacun des coins. Toutes les personnes sont reliées entre elles par une ligne. Le schéma s’intitule « Communication ». À gauche de la table, il est écrit « Dimension sociale » dans un rectangle bleu, et à droite de la table, il est écrit « Dimension conceptuelle » dans un rectangle violet. Entre les personnes assises au nord et à l’ouest, il est écrit « Enseignement au dialogue » dans un rectangle violet. Entre les personnes assises à l’ouest et au sud, il est écrit « Considération des propos des autres » dans un rectangle violet. Entre les personnes assises au nord et à l’est, il est écrit « Syntaxe et symboles » dans un rectangle bleu. Et entre les personnes assises à l’est et au sud, il est écrit « Arguments mathématiques » dans un rectangle bleu.La communication est un élément essentiel dans l’apprentissage des mathématiques. C’est une habileté qui va au-delà de l’utilisation appropriée de la terminologie et des symboles mathématiques dans une communication verbale ou écrite. C’est aussi, de façon plus importante, un véhicule par lequel les élèves acquièrent une compréhension des concepts mathématiques dans des contextes qui font appel à des raisonnements et à des arguments mathématiques. C’est ce que Radford et Demers (2004) appellent la dimension conceptuelle de la communication.
Ces chercheurs soulignent aussi l’importance de prendre en compte la dimension sociale de la communication. En effet, qui dit communication dit échange entre deux personnes ou plus. L’échange sera profitable pour toutes les personnes impliquées, dans la mesure où il règne au sein du groupe un climat propice au dialogue et une culture de respect et d’écoute.
Pour accroître l’efficacité de l’enseignement du domaine Nombres, le personnel enseignant doit favoriser l’émergence d’une culture qui valorise la communication comme moyen d’appropriation du savoir. Il doit donc créer des occasions propices aux échanges entre les élèves afin de les pousser à préciser leurs raisonnements et leurs stratégies. La communication est au centre de toutes les situations d’apprentissage.
Rôle des représentations dans l’apprentissage des mathématiques
En mathématiques, la communication n’est pas uniquement une affaire de mots. Les idées doivent être véhiculées au moyen de différents modes : concret (par exemple, avec des réglettes), semi-concret (par exemple, avec une droite graduée ou un schéma), symbolique (par exemple, en utilisant des chiffres et des symboles mathématiques dans une équation) et, bien sûr, verbal, à l’aide de mots, qu’ils soient lus, vus, dits, écrits ou entendus.
Ces divers modes de représentation présentés dans le schéma ci-dessous permettent d’exploiter plusieurs entrées cognitives, établissant ainsi des liens entre les idées, liens indispensables à l’apprentissage. Le personnel enseignant utilise des modèles pour représenter des concepts mathématiques aux élèves qui, à leur tour, s’en servent pour résoudre des problèmes et clarifier leur pensée.
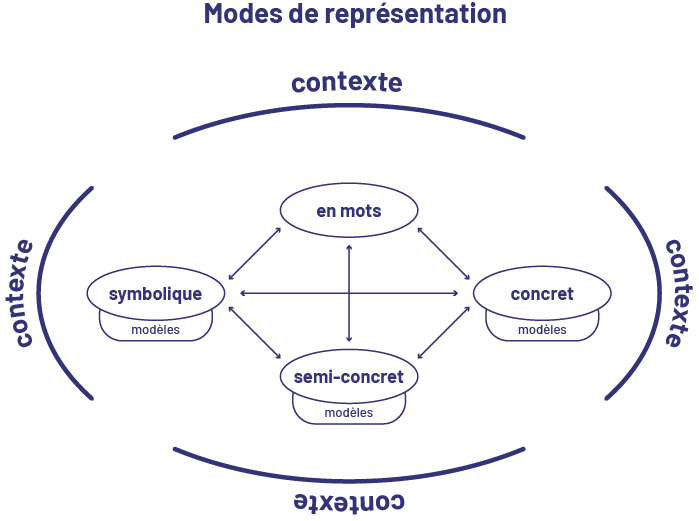 image Le schéma s’intitule « Modes de représentation ». En haut, en bas, à gauche et à droite, il y a quatre arcs qui, sans se toucher, forment une espèce d’ovale. Au-dessus du sommet de chaque arc est écrit le mot « contexte ». Sous chaque creux d’arc apparaissent différents termes, disposés en forme de losange, chacun écrit dans un ovale. En haut, l’ovale contient l’expression « en mots ». À droite, l’ovale contient le mot « concret ». Sous cet ovale est écrit le mot « modèles ». En bas, l’ovale contient le mot « semi-concret ». Sous cet ovale est écrit le mot « modèles ». Et à gauche, l’ovale contient le mot « symbolique ». Sous cet ovale est écrit le mot « modèles ». Tous les termes sont reliés les uns aux autres par des flèches à double sens.
image Le schéma s’intitule « Modes de représentation ». En haut, en bas, à gauche et à droite, il y a quatre arcs qui, sans se toucher, forment une espèce d’ovale. Au-dessus du sommet de chaque arc est écrit le mot « contexte ». Sous chaque creux d’arc apparaissent différents termes, disposés en forme de losange, chacun écrit dans un ovale. En haut, l’ovale contient l’expression « en mots ». À droite, l’ovale contient le mot « concret ». Sous cet ovale est écrit le mot « modèles ». En bas, l’ovale contient le mot « semi-concret ». Sous cet ovale est écrit le mot « modèles ». Et à gauche, l’ovale contient le mot « symbolique ». Sous cet ovale est écrit le mot « modèles ». Tous les termes sont reliés les uns aux autres par des flèches à double sens. Modèles mathématiques
Depuis longtemps, les spécialistes des mathématiques construisent des modèles pour expliquer et représenter des découvertes et des observations du monde, et pour les communiquer efficacement. Par exemple, en pensant à un nombre, certaines et certains le visualisent dans un modèle mathématique tel que la droite numérique ouverte ou une grille de nombres. Cela aide à mieux cerner le nombre et à reconnaître qu’il est plus que…, moins que… ou près de… un autre nombre. Les modèles sont donc des représentations d’idées mathématiques.
Le jeune enfant visualise le monde qui l’entoure à sa façon. Pour dessiner l’arbre devant sa maison, elle ou il trace des lignes sur du papier et le représente en deux dimensions, et ce, même si l'enfant l’a touché, en a fait le tour et s’est abrité sous ses branches (Fosnot et Dolk, 2001, p. 74). Cette représentation n’est pas une copie de l’arbre, mais bien une construction de ce qu’elle ou il connaît. C’est en fait « un modèle » de l’arbre. Il en va de même pour les élèves dont les premiers modèles utilisés pour résoudre des problèmes reflètent leur interprétation de la réalité.
Toujours selon Fosnot et Dolk (2001, p. 80), les modèles, tout comme les grandes idées et les stratégies, ne peuvent être transmis automatiquement, mais font l’objet d’une réappropriation et d’une construction de la part des élèves. La table de valeurs en est un bon exemple : intuitivement, les élèves « organisent » les données numériques en les plaçant de façon disparate sur une feuille, mais la table de valeurs permet de les ordonner en vue de les traiter et de les analyser.
Cependant, une précision au sujet des modèles et du matériel de manipulation est de mise : le modèle n’est pas l’idée mathématique. De ce fait, l’arbre que l’enfant a dessiné, dans l’exemple plus haut, n’est pas un arbre, mais une représentation de la situation qui servira à en discuter. Il en va de même pour tous les modèles employés.
Le matériel de base dix est un modèle, car il suppose que la personne qui l’utilise possède déjà une compréhension du concept de regroupement. Cependant, présenter une languette d’une trousse de matériel de base dix et affirmer qu’il s’agit d’une dizaine est faux. L’objet n’est pas une « dizaine », mais un moyen concret de représenter « l’idée » de la dizaine. Ici, il représente une dizaine de petits cubes, mais il pourrait représenter une unité, un arbre ou même une poutre. Selon l’intention, il pourrait aussi représenter un dixième, par exemple, en représentant le nombre 2,5 avec 2 planchettes (2 unités) et 5 languettes (5 dixièmes).
La droite numérique est un autre modèle auquel il faut exposer les élèves. La droite numérique ne représente pas la quantité correspondant aux nombres qui sont placés sur cette droite; elle permet de « voir » les nombres en relation les uns avec les autres. Par exemple, une droite numérique sur laquelle les nombres 44, \(42\frac{3}{4}\) et 41,5 sont placés représente la relation d’ordre entre ces trois nombres.

Dans le but de favoriser le raisonnement des élèves, le personnel enseignant doit utiliser divers modèles et les inciter à faire de même. Les modèles ne devraient pas nécessairement faire l’objet d’un enseignement formel; ils peuvent être présentés dans le cadre de situations de résolution de problèmes. Par exemple, la droite numérique est un excellent modèle pour explorer l’addition de plusieurs nombres. Cependant, la majorité des élèves ne « conçoivent » pas qu’elle puisse être créée sans qu’elle soit graduée. Imaginons alors un échange mathématique, dans le cadre d’un problème d’addition, où ils présentent leurs stratégies de résolution de problèmes. Le personnel enseignant pourra en profiter pour faire un lien entre la droite numérique utilisée par l'élève (Figure 1) pour effectuer une opération et la possibilité d’utiliser une droite numérique ouverte (Figure 2).
Exemple
\(\ 5 + 3 + 10\)
 image La Figure un est une droite numérique graduée par unités qui indique les points zéro, cinq, huit et 18. La figure deux est une ligne de dénombrement qui n’indique que les points cinq, huit et dix-huit. Une flèche courbe va de cinq à huit et indique « plus huit ». Une flèche courbe va de huit à 18 et indique « plus dix ».
image La Figure un est une droite numérique graduée par unités qui indique les points zéro, cinq, huit et 18. La figure deux est une ligne de dénombrement qui n’indique que les points cinq, huit et dix-huit. Une flèche courbe va de cinq à huit et indique « plus huit ». Une flèche courbe va de huit à 18 et indique « plus dix ».De même, afin de représenter des situations impliquant des fractions, les élèves tendent souvent à utiliser un modèle de surface (par exemple, cercle ou rectangle). Cependant, ce type de modèle ne permet pas de représenter fidèlement des situations où le tout est une longueur ou une distance. Le personnel enseignant peut alors profiter d’une occasion où les élèves utilisent un modèle de surface pour représenter la fraction d’une longueur et leur montrer comment un modèle de longueur (par exemple, une droite numérique) serait plus approprié.
Il faut exposer les élèves à une multitude de représentations pour qu’elles et ils soient en mesure d’établir des liens entre elles et consolider leur apprentissage. Au cours de leur scolarisation, les élèves doivent vivre une transition à partir de l’utilisation d’un modèle comme outil didactique dans une situation particulière vers l’utilisation d’un modèle comme stratégie pour généraliser des idées mathématiques, pour résoudre des problèmes et pour appliquer le modèle à de nouveaux contextes. Cette transition d’un contexte familier à un nouveau contexte constitue une étape fondamentale dans l’apprentissage des mathématiques. Elle se trouve dans la grille d’évaluation du rendement du programme-cadre de mathématiques, sous la compétence « Mise en application ».
Voici quelques modèles que les élèves peuvent utiliser dans le domaine Nombres :
- la droite numérique;
- la droite numérique ouverte;
- la disposition rectangulaire;
- la table de valeurs;
- la grille de nombres;
- le matériel de base dix;
- l’équation;
- le modèle de surface pour représenter des fractions;
- le modèle de longueur pour représenter des fractions;
- le modèle d’un ensemble pour représenter des fractions;
- le modèle de volume pour représenter des fractions;
- la monnaie pour représenter des nombres décimaux.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 8-12.
Enseignement de la résolution de problèmes
« L’activité de résolution de problèmes et l’apprentissage sont intimement liés; les élèves apprennent les mathématiques en faisant des mathématiques. »
(Van de Walle et Folk, 2005, p. 44, traduction libre)
 image Le schéma s’intitule « Enseignement par la résolution de problèmes ». Un cercle est constitué de plusieurs anneaux emboîtés l’un dans l’autre. Dans l’anneau extérieur, le plus large, il est écrit « Situations d’apprentissage engageantes ». Dans le suivant, il est écrit « Questionnement et réflexion ». Dans le suivant, il est écrit « Stratégies personnelles ». Et dans le dernier, il est écrit « Échange mathématique ». Un autre cercle se superpose à celui-ci et il y est écrit : « Compréhension des concepts et des processus ».
image Le schéma s’intitule « Enseignement par la résolution de problèmes ». Un cercle est constitué de plusieurs anneaux emboîtés l’un dans l’autre. Dans l’anneau extérieur, le plus large, il est écrit « Situations d’apprentissage engageantes ». Dans le suivant, il est écrit « Questionnement et réflexion ». Dans le suivant, il est écrit « Stratégies personnelles ». Et dans le dernier, il est écrit « Échange mathématique ». Un autre cercle se superpose à celui-ci et il y est écrit : « Compréhension des concepts et des processus ». Afin d’aider les élèves à bien comprendre les concepts et les processus du domaine Nombres, il est important de les placer en situation de résolution de problèmes dès le début d’une unité d’apprentissage. Lorsqu’elles et ils travaillent en équipe pour résoudre un problème engageant et non routinier, les élèves deviennent habiles à formuler une hypothèse et un argument mathématique. Elles et ils apprennent aussi à prendre des risques, à persévérer et à avoir confiance en leur capacité à résoudre des problèmes. C’est dans un tel contexte que l’apprentissage des mathématiques prend tout son sens.
L’enseignement par la résolution de problèmes exige que le personnel enseignant présente des situations d’apprentissage qui soutiennent l’intérêt des élèves. Le contexte ou la situation du problème devient alors un facteur déterminant. « Les problèmes proposés devraient partir de contextes réels (c’est-à-dire des situations qui se produisent de façon authentique en salle de classe), de contextes réalistes (c’est-à-dire des situations qui sont issues d’expériences qui pourraient être vécues par les élèves à l’extérieur de la salle de classe) et même de contextes fantaisistes (c’est-à-dire des situations qui font appel à l’imaginaire des élèves) » (Vézina et coll., 2006, p. 4). De fait, le contexte peut être un élément accrocheur pour les élèves et leur donne une raison de « faire des mathématiques ». Conséquemment, le contexte doit être choisi, formulé et façonné judicieusement afin de toucher leur sensibilité. Le contexte est donc un élément de la résolution de problèmes qui peut être utilisé afin de susciter l’intérêt des élèves.
L’enseignement par la résolution de problèmes exige aussi que le personnel enseignant présente aux élèves des situations d’apprentissage riches en contenu mathématique qui les incitent à réfléchir. Il doit ensuite laisser les élèves élaborer leurs propres stratégies de résolution de problèmes sans trop les diriger. Enfin, le personnel enseignant doit clarifier les concepts mathématiques lorsque les élèves présentent leurs stratégies et leurs solutions lors de l’échange mathématique. L’échange mathématique est en quelque sorte un temps d’objectivation au cours duquel les élèves expliquent et défendent leur raisonnement et analysent celui des autres. L’apprentissage et la compréhension se forgent grâce à cette confrontation d’idées et à un questionnement efficace de la part du personnel enseignant. En outre, l’échange mathématique permet aux élèves de consolider leurs apprentissages et de développer diverses habiletés telles que l’habileté à résoudre des problèmes, à communiquer, à raisonner, à écouter et à analyser.
« Au cours de l’échange mathématique, les apprenantes et les apprenants – de jeunes mathématiciennes et mathématiciens au travail – défendent leur raisonnement. Des idées et des stratégies ressortent de la discussion et contribuent à former le bagage mathématique des élèves de la classe. »
(Fosnot et Dolk, 2001, p. 29, traduction libre)
L’enseignement par la résolution de problèmes est axé sur la compréhension. Dans le domaine Nombres, les élèves résoudront des problèmes pour acquérir un meilleur sens des opérations, lequel se traduira par l’emploi de stratégies comprises et non par l’emploi d’étapes mémorisées et appliquées aveuglément.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 13-14.
