C2.2 Déterminer si des ensembles d’expressions qui comportent des additions, des soustractions, des multiplications et des divisions sont équivalents ou non.
Habileté : déterminer si des ensembles d’expressions comportant les quatre opérations sont équivalents ou non
Deux expressions numériques sont équivalentes lorsqu’elles représentent la même quantité.
Par exemple, en représentant les expressions 3 × 4 et 2 × 6 avec des réglettes, l’élève constate qu’elles sont équivalentes puisqu’elles représentent la même quantité.
Deux expressions numériques ne sont pas équivalentes lorsqu’elles représentent des quantités différentes. Dans une phrase mathématique, l’utilisation du signe d’égalité traversé par une barre oblique (≠) est un symbole qui représente cette non-équivalence ou deux quantités différentes.
Le signe d’égalité ne doit pas être considéré comme un symbole qui annonce la réponse d’une équation, mais comme un symbole qui montre une relation entre deux quantités.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
En raisonnant algébriquement, les élèves analysent les nombres, les symboles, les quantités, les opérations, puis les généralisent.
Une étape mathématique significative dans le développement de la pensée algébrique est de comprendre qu’une situation d’égalité peut être représentée à l’aide de différents modèles.
Les élèves peuvent utiliser différents modes de représentation. Les relations mathématiques peuvent être représentées à l’aide de matériel concret ou semi-concret, de symboles ou de descriptions orales. Lorsque les élèves représentent une situation algébrique à l’aide d’un ou de deux modes de représentation, elles et ils utilisent une variété de modèles tels que des tableaux, des grilles de nombres ou des droites numériques. Ces modèles les aident à organiser, à enregistrer et à communiquer leur réflexion quant à des situations d’égalité. La représentation d’expressions numériques à l’aide de modèles concrets, semi-concrets ou symboliques, de pair avec une description orale, facilite l’observation de relations et contribue au développement de la pensée algébrique. Les différentes représentations permettent aux élèves de s’approprier les concepts algébriques.
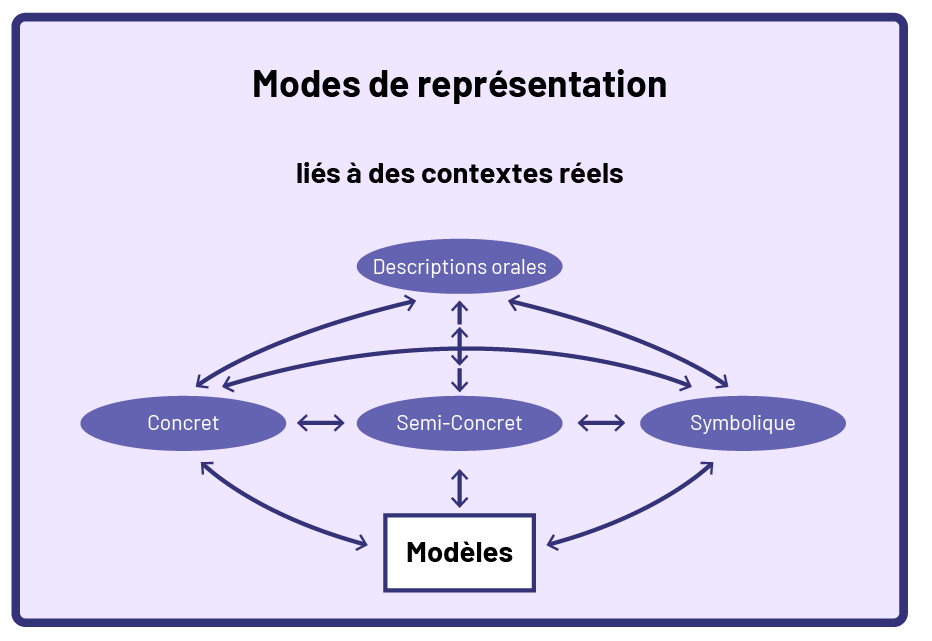
Il est primordial que les élèves explorent et représentent des relations d’égalité de diverses façons avant de les exprimer symboliquement par une phrase mathématique. Une phrase telle que 20 + 15 = 35 perd tout son sens lorsque l’accent est d’abord mis sur les symboles utilisés. Avant d’exécuter des calculs, les élèves doivent explorer les nombres à l’aide de modèles pour appuyer leur raisonnement. Le sens du symbole s’acquiert par l’utilisation de diverses représentations de relations d’égalité et d’inégalité. Le questionnement du personnel enseignant, conjugué à la manipulation des symboles et des nombres selon différentes stratégies, permettra aux élèves de proposer des conjectures et, par la suite, de généraliser.
En algèbre, les élèves doivent s’approprier le concept d’égalité et d’inégalité afin de bien comprendre l’équivalence en tant que relation entre deux quantités. Les élèves doivent d’abord explorer ces concepts avec du matériel concret.
Devant une situation d’égalité représentée par des symboles, le personnel enseignant doit amener les élèves à reconnaître la relation qui existe entre les deux expressions numériques de chaque côté du signe =. Par exemple, dans la phrase mathématique 18 = 6 × 3, le 18 et le 6 × 3 constituent deux représentations du nombre 18 et le signe = est le symbole qui montre la relation d’égalité entre ces représentations. Bien comprendre cette relation permettra, par la suite, aux élèves de manipuler plus efficacement les nombres ou les variables qui figurent dans une équation.
La vidéo suivante clarifie la relation d’égalité entre deux expressions numériques.
 Description de la vidéo
Description de la vidéo
Description à venir
Sens du symbole de l’égalité
Le symbole de l’égalité est un signe universellement connu, mais souvent mal interprété par plusieurs élèves qui perçoivent le signe = comme le symbole qui précède toujours, dans les phrases mathématiques, la réponse à un calcul de gauche à droite.
Par la suite lorsque les élèves explorent la représentation symbolique d’une situation d’égalité ou d’équivalence, par exemple l’équation 4 + 3 = □ + 2, les élèves croient que le nombre 7 doit être inséré dans la case de l’inconnue, puisqu’il représente la réponse à l’opération 4 + 3, figurant à gauche du signe =. Lorsqu’on leur demande de traiter le nombre 2, les élèves l’ajoutent au 7, comme si la phrase mathématique se poursuivait simplement de gauche à droite : 4 + 3 = 7 + 2. Les élèves ne perçoivent pas le signe = comme le symbole de la relation d’égalité ou d’équivalence entre les expressions figurant de part et d’autre de ce signe.
Cette fausse conception vient en partie du fait que les élèves voient souvent des situations d’égalité présentées par de simples phrases mathématiques telles que 4 + 1 = 5. Pour remédier à cette méprise, le personnel enseignant peut :
- demander aux élèves : « Est-ce que 14 + 6 représente la même quantité que 6 + 14 ? »;
Note : Ce type de questionnement favorise une meilleure compréhension des concepts de relation et d’égalité.
- présenter différents types de phrases mathématiques pour permettre aux élèves d’explorer le concept du signe = en tant que relation.
En voici quelques-unes :
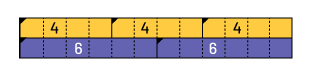
- Phrase ne présentant qu’un nombre de part et d’autre du signe =, par exemple 5 = 5
- Phrase incitant au recours d’une stratégie, par exemple la stratégie comparer des termes
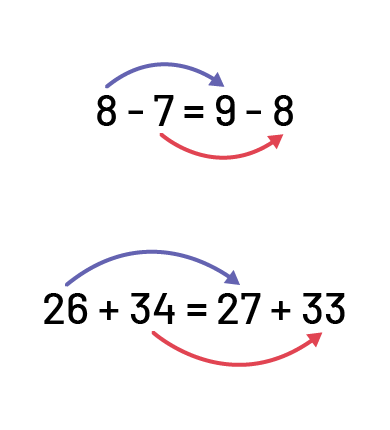
- Phrases qui recourent à une propriété, par exemple la propriété de commutativité : 5 + 10 = 10 + 5;
- Phrases dont l’une des expressions numériques présente plus de deux termes, par exemple 5 = 2 + 2 + 1 ou 55 = 25 + 25 + 5;
- Phrases dont les opérations diffèrent de chaque côté du signe =, par exemple 29 + 2 = 33 – 2.
Le signe = représente la relation entre les expressions et non le symbole qui précède systématiquement la réponse à une opération.
Il est important d’encourager les élèves à exprimer, de façon explicite, leur propre compréhension du signe =. Ces échanges permettront au personnel enseignant de vérifier cette compréhension et aux élèves d’utiliser des arguments mathématiques, une des assises de la pensée algébrique.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 36-39.
Habileté : rétablir une situation d’égalité
Pour développer le raisonnement algébrique, il est aussi important que les élèves explorent des situations d’inégalité. Ces situations requièrent le recours à des stratégies qui visent à rétablir l’égalité (la rendre vraie) et exigent un niveau de pensée plus élevé (analyse). Rétablir l’égalité d’une situation s’effectue d’abord à l’aide de matériel concret (par exemple, avec des tours de cubes, des cadres à 10 cases, des réglettes, des balances), puis à l’aide de symboles.
Exemple à l’aide de matériel concret
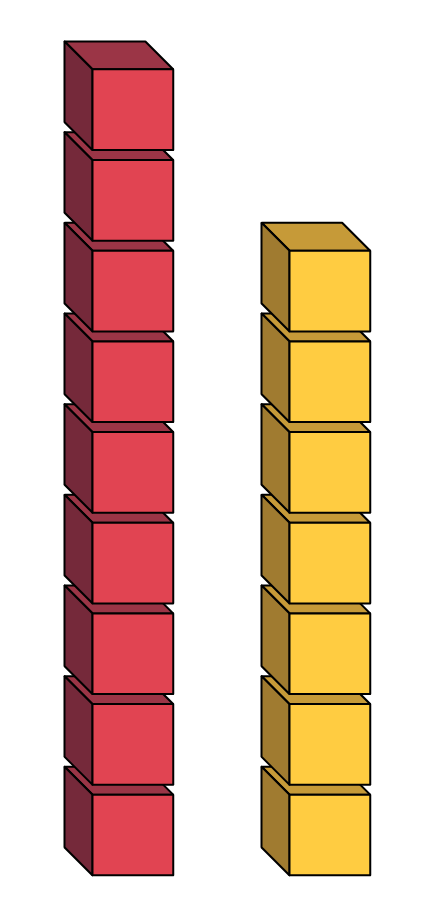
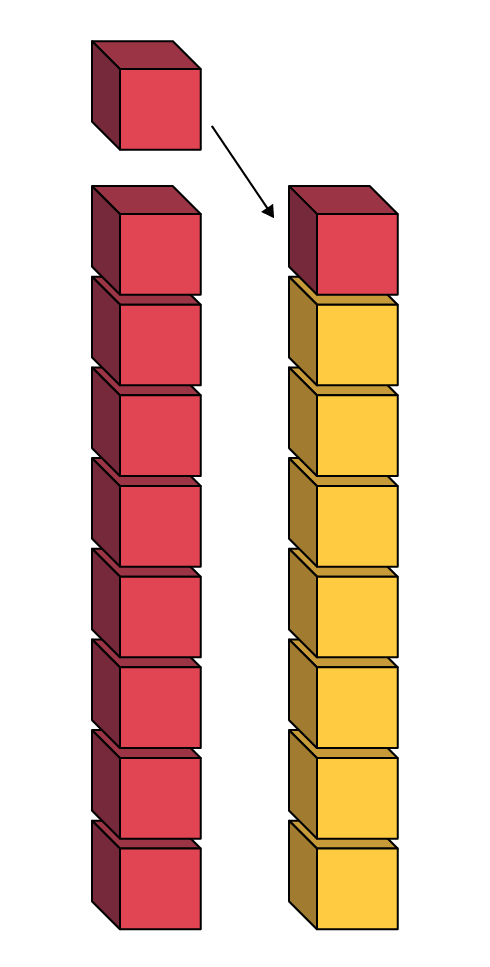
Exemple à l’aide de symbole
23 + 14 ≠ 14 + 21.

Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 44-45.
Connaissance : expression numérique
Expression qui ne contient que des nombres liés entre eux par des opérations. Tous les nombres sont, par définition, des expressions numériques.
Exemples
3 + 9 – 2
5 × 4
10
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 32.
Connaissance : paires d’expressions numériques équivalentes
Deux expressions numériques sont équivalentes lorsqu’elles représentent la même quantité.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Par exemple, en observant un bond de 5 et un bond de 20 sur une droite numérique et un bond de 20 et un bond 5 sur une autre droite numérique, l’élève constate que l’expression 5 + 20 est équivalente à 20 + 5 puisque la somme des deux expressions représente une quantité de 25.
