C2.3 Solve equations that involve multiple terms and whole numbers in various contexts, and verify solutions.
Skill: Solving Equations
Different Types of Equations
An equation is a symbolic way of representing an equality. In the junior grades, students encounter the following four types of equations:
- Equation with one variable: An equation such as 2 + n = 14 is solved to determine the value of the variable that makes the equation hold true.
- Equation with two variables: An equation such as c = 2n + 3 is used to express a relationship, such as the relationship between the term number (n) and the term value (c). The values for c are dependent on the values for n. This equation has multiple solutions.
- Equation that is a formula: A formula such as A = c × c can be used to represent the area (A) of any square, where c represents the side length. The area of a particular square can be determined by substituting a side length into the formula. The side length of a particular square can be determined by substituting the area for that square into the formula.
- Equation that generalizes a property situation: The equality relationship between adding any two identical numbers and multiplying that number by two can be expressed using the equation n + n = 2 × n. This equation can be verified by testing that the equation holds true for various values of n, such as 4 + 4 = 2 × 4.
Note: The details of the various types of equations are given in order to recognize that algebraic concepts are not encountered and treated exclusively in the context of modeling and algebra activities. For example, equations that are used as formulas in measurement are regularly found. However, in the junior grades, students do not necessarily have to distinguish between these types of equations.
Each of these types of equations is discussed in more detail in the following:
Solving Equations with One Variable
In the primary grades, students usually solve equations in the Algebra and Number strands. These equations are usually derived from word problems and are often solved using concrete representations and illustrations.
In the junior grades, students are more likely to solve equations using a variety of strategies. It is essential that students master the concept of equality as an expression of equilibrium before they begin to solve equations.
Solving such equations means determining the value of the unknown that maintains the equality. Solving equations must be done in a context of understanding and analyzing the equality. It is therefore important to regularly invite students to explain their approach to solving, to justify their actions and to demonstrate their understanding of the concepts involved in order to prevent solving equations from becoming just a blind application of procedures.
Solving Equations by Systematic Testing (Trial and Error)
In this strategy, students systematically choose potential values of the unknown value and test until one of these values makes the equality true. To solve, for example, the equation 2 × p + 6 = 22, they successively choose p = 1, 2, 3… and find that the equality is true when p = 8.
To solve certain equations, such as 125 - b = 32, students can use number sense strategies to reduce the number of trials. For example, to solve this equation, it would not be wise to proceed using b = 1, b = 2, b = 3, and so on, because that would take too much time. They might think like this: "I know that 125 - 100 = 25, and 25 is close to 32. If I subtract 105, I get 20. I am getting away from the quantity I am looking for. So I'll subtract a little less than 100. I'll try b = 99, b = 98, and so on."
Advantages of solving equations by systematic testing:
- Students highlight what it means to solve an equation, in other words, to determine the value of the variable that maintains equality.
- Students work systematically, not randomly. They can also use their sense of numbers.
Disadvantage of solving equations by systematic testing:
- Communication of work done can be disorganized, as it can be difficult to keep track of trials. Students can then be encouraged to keep such records by creating a table of values.
Here is an example of a table of values used to solve the equation 125 - b = 32:
| b | 100 | 105 | 99 | 98 | 95 | 93 |
|---|---|---|---|---|---|---|
| 125 - b | 25 | 20 | 26 | 27 | 30 | 32 |
Note: Some notations should be avoided. For example, to solve the equation 2 × p + 6 = 22, the student who tries p = 1 should not write "2 × 1 + 6 = 22," since this equality is false. Students can evaluate the left-hand side of the equation to get 2 × 1 + 6 = 8 or use the equation in interrogative form (for example, 2 × 1 + 6 22) or write 2 × 1 + 6 ≠ 22.
Solving Equations by Inspection
In this strategy, students recognize the equality relationship represented by the equation. Students compare the quantities involved and use their number sense to determine the value of the unknown. Here are three examples of solving the equation c + 45 = 98 by inspection:
Example 1
A student recognizes that he needs to find the number that, when added to 45, adds up to 98. To do this, he uses his number sense. Since he knows that 45 + 45 = 90, he concludes that the number he is looking for is 8 more than 45, or 53.
Example 2
A student recognizes that if you take away the same quantity on each side of the equality, the equation is changed, but the equality is maintained.
c + 45 = 98
c + 45 - 45 = 98 - 45
c = 98 - 45
c = 53
Note: It is important that students do this reasoning in steps, otherwise they may simply apply a misunderstood procedure mechanically. In addition, this reasoning can be used to better grasp the concept of inverse operation, in other words, subtraction is the inverse operation of addition.
Example 3
A student decomposes a number, then compares or cancels the numbers.

Advantages of solving equations by inspection:
- Students practice decoding the equation, that is, making sense of the symbolism of the equation. Students develop their sense of symbol, equation and equality.
- Students think about operations and numbers instead of trying to use a meaningless procedure.
In the examples above, one can recognize that students can solve the same equation by inspection using a variety of strategies. The strategies comparing terms, decomposing terms, and modifying the equation, which were explored during the analysis of an equality, apply very well in situations involving solving equations by inspection, since the equation represents an equality. Teachers should help students make this connection by pointing out the similarity between an equality and an equation to solve.
Equation that Represents a Relationship Between Two Changing Quantities
Students learn to represent relationships between the term number and the term value by equations. Students can substitute either the term value or the term number into the equation to determine the value of the unknown.
A table of values can be used to verify the solution.
Example
For the pattern below, what is the relationship between the term number and the number of points?
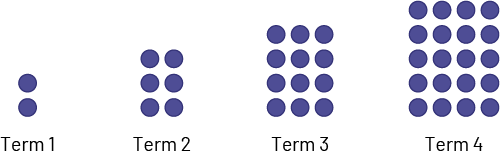
Students might represent the relationship using the equation p = n ×(n + 1), where n is the term number and p is the number of points in it. The table of values below also represents this relationship.
| Term Number (n) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Number of Points (p) | 2 | 6 | 12 | 20 | 30 | 42 | 56 | 72 | 90 | 110 |
Students can make connections between the equation and the table of values. For example, if n = 1, the equation becomes p = 1 × (1 + 1), hence p = 2, which matches the data in the table. If n = 3, the equation becomes p = 3 × (3 + 1), hence p = 12, which also corresponds to the data in the table. Thus, the question "how many points does term 9 have?" can be expressed by the statement "solve the equation p = 9 × (9 + 1)". To solve it, students can use the table of values by looking for the value of p for which n = 9 or perform the calculation and determine that p = 90.
Similarly, a question such as "What term number has 72 points?" can be expressed as "Solve the equation 72 = n ×(n + 1)" because in the equation p = n ×(n + 1), p takes a value of 72. To solve it, students can look in the table of values for the value of n for which p = 72 and conclude that n = 8.
Equation as a Formula
In the Spatial Sense strand, students learn to represent area and volume using formulas. For example, students discover that the area of a rectangle can be found by multiplying the length of the base by the height of the rectangle. Students can generalize this area formula, as A = b × h or A = L × l.
Formulas usually involve multiple variables. To solve for a particular variable, values are substituted into the other variables before the equation is solved for the one unknown value. For example, the question "What is the height of a rectangle that has a base of 8 cm and an area of 72cm2?" can be translated into algebraic language as "Solve the equation 72 = 8 × h ".
Equation that Generalizes a Situation of Equality
Students may encounter these types of equations in particular when exploring the properties of numbers and operations (for example, m - m = 0). These equations symbolically express the fact that a situation of equality is always true, regardless of the values of the variable(s) that make up the equation(s), and regardless of whether they are natural numbers, fractions, or decimal numbers.
Beginning in the primary grades, students explore certain properties of numbers and operations (for example, the property of 0 in addition, the commutativity of addition) and make conjectures about these properties using words. In the junior grades, students continue to explore properties and progress to making generalizations using words or an equation. It is important to note, however, that using an equation to generalize a situation of equality requires a good deal of abstraction. Only after developing a good understanding of properties are students able to fully grasp the meaning of such equations.
Here are some examples of properties of numbers and operations that are expressed in words and using an equation:
Equality Situation
0 + 2230 = 2230
0 + 9.72 = 9.72
Generalization Using Words
"When you add any number to 0, you get that number."
Generalization Using an Equation
0 + m = m
Equality Situation
\(776 - 0 = 776\)
\(\frac{3}{4} - 0 = \frac{3}{4}\)
Generalization Using Words
"When we subtract 0 from any number, we get that number."
Generalization Using an Equation
m - 0 = m
Equality Situation
0 × 15 = 0
\(0 \times \frac{3}{4} = 0 \)
Generalization Using Words
"When we multiply 0 by any number, we get 0."
Generalization Using an Equation
0 × n = 0
Equality Situation
1 × 235 = 235
1 × 1.56 = 1.56
Generalization Using Words
"When we multiply 1 by any number, we get that number."
Generalization Using an Equation
1 × n = n
Equality Situation
4 + 3 = 3 + 4
Generalization Using Words
"When adding two numbers, the order in which you add them is not important."
Note: In the junior grades, teachers can lead students to recognize that this property also applies to the sum of more than two numbers.
Generalization Using an Equation
a + b = b + a
Teachers need to support students' journey toward an understanding of equations that generalize an equality situation. The example below describes a step in this direction that leads to the generalization of the distributivity property of multiplication over addition:
Example
Using concrete materials, demonstrate to students that in order to calculate 3 × 24, one can calculate 3 × 20 and 3 × 4 separately, and then sum the products.
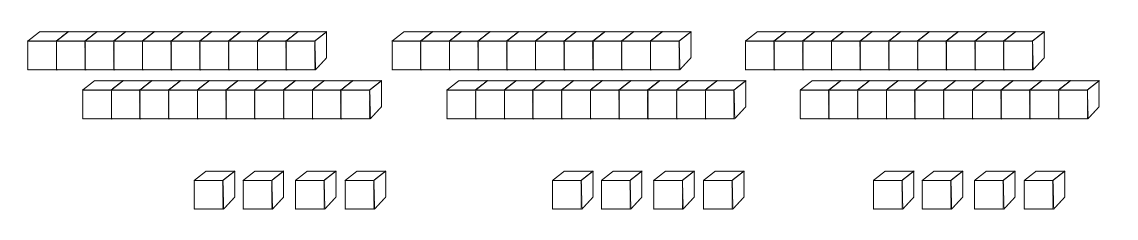
Next, introduce students to various equalities that relate to the distributivity property of multiplication over addition.
Example
4 × 27 = (4 × 20) + (4 × 7)
11 × 34 = (11 × 30) + (11 × 4)
For each, have students explain, represent, and analyze the property by asking thought-provoking questions such as:
- Is the equality true? How do you know?
- Can you demonstrate this with concrete materials?
- Can you verify the equality without doing any calculations?
- Would it work with other numbers?
- Can you represent the equality using a rectangular layout?
Throughout the exploration, encourage students to make conjectures related to the equalities presented, such as, "When a number is multiplied by another number, the second number can be decomposed before it is multiplied by the first."
Then introduce students to equations that use distributivity and can be solved easily without performing calculations. For example:
Example
7 × 31 = (7 × □) + (7 × 1)
6 × 28 = (□ × 20) + (6 × 8)
7 × 9 = (3 × 9) + (□ × 9)
(20 × 8) + (□ × 8) = 23 × 8
Ask questions that lead students to a generalization that the distributivity property of multiplication over addition is true regardless of the numbers used. Ask them to symbolically represent this property with an equation, for example, a ×(b + c) =(a × b) +(a × c).
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 89-97.
Knowledge: Equation
A mathematical statement that has equivalent expressions on either side of an equal sign.
Example
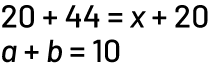
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Knowledge: Variable
A symbol or letter in an equation can represent an unknown value that makes the equality hold true.
Example
In the equation, 10 = Δ + 9, the triangle is a variable, because the value is unknown. We can replace it with a single value, namely 1, to make the equation true.
In the equation 10 = Δ + * or 10 = x + y, the symbols or letters are variables, as they can be replaced with different values.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
