C2.3 Identify and use equivalent relationships for whole numbers up to 50, in various contexts.
Skill: Determining and Using Equivalence Relationships Involving Numbers Up To 50
Developing algebraic thinking is a complex process that relies on three fundamental processes: abstracting, generalizing, and operating on the unknown.
Note: Although properties of operations, such as the commutative property, are explored and applied in the Number strand, the process of coming to understand and generalize them falls under algebraic thinking.
Generalizing
Generalizing is drawing valid conclusions, true in all cases, from the observation and analysis of a few examples (adapted from Squalli, 2002, p. 9).
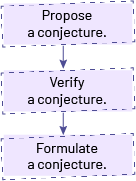
In situations of equality, students can more easily formulate a generalization when it follows a process of proposing and verifying a conjecture.
A conjecture is the expression of an idea that is perceived to be true in any similar situation.
When students see a recursive phenomenon while exploring various equality situations, they are able to propose a conjecture; for example, they might say that if you add the number 0 to any number, the initial quantity does not change.
Students should then check whether their conjecture is valid in other similar situations. For example, in the situation in the previous example, they could check it with various numbers as well as with concrete materials.
When a conjecture seems to apply to all similar situations, students formulate a generalization in words or using symbols.
Example 1
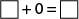
There are three important steps in the generalization process.
In the Primary and Junior Divisions, conjectures are usually expressed in words. They may also be represented using concrete or visual (semi-concrete) materials to illustrate their mathematical reasoning as clearly as possible.
Teachers should expose students to a variety of problem situations that challenge them to practice the skill of making and testing a conjecture; for example, they present the number sentence (50 + 6 – 6 = 50) and ask them what they notice. Then, they offer them the following conjecture: "I wonder, when you add and subtract the same number in a number sentence, if it is the same as when you add or subtract zero." Teachers then invite students to discuss this conjecture with each other and determine if it is still true.
Students test this conjecture with other number sentences. They may not be convinced that it applies to any number sentence or to all numbers, especially large numbers. In the course of the discussion, they can propose their own conjectures as illustrated below.

After a check of various number sentences, students can conclude that the conjecture is true and formulate a generalization.
Example 2

Since students' vocabulary in elementary school is not yet very developed and precise, initial conjectures usually need to be rephrased or clarified. Ideally, therefore, the formulation of a conjecture should be practiced in a class setting, as shown in the example below. During the discussion, students can point out the limitations of a peer's conjecture and contribute to the formulation of a clearer and more relevant common conjecture. However, it is important for teachers to establish a learning environment in which students perceive each other's questions as positive interactions that can fuel the exchange.
Example 3
Teachers present the number sentence (34 + 0 = 34) and ask students if it is true or false.
- Student: "It is true."
- Teacher: "How can you tell?"
- Student: "When a zero is added to a number, it doesn't actually add anything. Therefore, we get the starting number."
The teacher presents other similar number sentences. After several such exchanges, the teacher then asks students to formulate a conjecture.
- Student: "All numbers added with a zero remain the same."
- Another student presenting a counterexample: "No, because (10 + 30 = 40). The numbers 10 and 30 have zeros in them. When added together, they don't stay the same."
After further discussion, a student formulates another conjecture:
- Student: "When you add a zero to another number, you get the other number."
- Other student: "That's not true."
- Teacher: "So, are you referring to the number that is right next to the zero?"
- Student: "No, added to another number."
After much discussion, the following formulation is adopted: "Zero, when added to another number, is equal to that number." When students see that this conjecture applies to all numbers, they can generalize.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Fascicule 2, Situations d'égalité, p. 8-11.
The change from a concrete or semi-concrete representation (visual) to a symbolic one, and vice-versa, supports students in understanding the relations of equality.
Note: The commutative property is an example of an equivalence relation.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Skills Related to Equivalence Situations
In the primary grades, students develop the ability to recognize, explain, create, restore, and maintain equivalence through the application of strategies and models such as ten frames and the number line. These skills are refined with each grade using progressively larger numbers, consistent with curriculum requirements.
Initially, situations of equality and inequality are explored primarily with concrete materials and described verbally, and then students are gradually exposed to symbolic representation. However, the use of concrete materials always remains important and must be used in conjunction with the more abstract representations.
Skill: Recognizing a Situation of Equivalence
In a problem-solving approach, the use of concrete and visual (semi-concrete) materials, as well as models, helps students recognize and represent situations of equality and inequality.
Examples
Ten frame

Open double number line

Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Fascicule 2, Situations d'égalité, p. 40.
It is only after having manipulated various models several times with the goal of recognizing a situation of equality or inequality, that students will be able to approach the purely symbolic representation (the number sentence) of this situation. Furthermore, to determine the nature of the relationship between quantities, they must understand that the expressions on either side of the = sign are data to be analyzed, not just calculated.
Explaining a Situation of Equality
To develop their ability to explain a situation of equality, students must go through different stages. The transfer from the concrete to the symbolic representation is easier when the equality relationship is constructed by following these different steps.
1. Explore using concrete or visual (semi-concrete) materials
Using toys, a student illustrates the following situation: adding 0 toys to 10 toys.
2. Describe with words and materials
"If I add 0 toys to 10 toys, the quantity will not change, since I am not adding anything. It will still be equal to 10 toys."
3. To represent with symbols
The student can then express this equality symbolically by writing the number sentence 10 + 0 = 10.
4. Propose a conjecture
By exploring several similar situations, the student can assume that adding 0 never changes the quantity.
5. Generalize for all numbers
Appropriate questions during other similar situations lead the student to generalize that adding 0 to any quantity does not change the quantity.
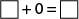
Students also develop their ability to explain a situation of equality by using models. Indeed, the use of models helps students communicate their reasoning effectively.
Example
To explain the expression 27 + 5 – 5 = 27, students can use an open number line to support their reasoning: "I take a leap of 27 and add a leap of 5. I take another leap of 5 in the other direction, so I am back to 27. It's like I never added a leap of 5."

Creating a Situation of Equality
To get students to create an equality situation, it is important to start by presenting them with an equality situation represented with concrete materials. Ask them to represent it with a number sentence, then gather and compare the different sentences proposed by the students and determine if they are all true.
Examples
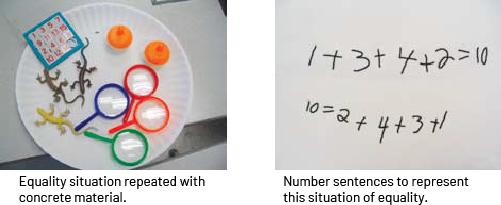
Afterwards, students can create their own equality situation. Ask them to represent them with concrete materials and number sentences. Students should have the opportunity to create equality situations represented by number sentences with larger numbers so that they use the properties of operations or strategies instead of calculations.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Fascicule 2, Situations d'égalité, p. 39-43.
Knowledge: Equivalence Relationship
The state of being equal or equivalent in value.
Example
352 is equivalent to 350 and 2.
Knowledge: Equality
The state of being equal.
Knowledge: Number Sentence
An equality or inequality that uses numbers and mathematical symbols, such as operation signs. A number sentence represents a relationship. In a number sentence, there is no unknown or variable.
Example
True (equal) sentences: \(75 + 5 = 5 + 75\) or \(50 = 20 + 20 + 10\)
False (unequal) sentences: \(100 = 95 - 5\) or \(45 + 10 = 15 + 45\)
