La vue d'ensemble

À vue d'oeil...

Un remaniement des guides d'enseignement efficace en mathématiques

D2.1 Utiliser le vocabulaire mathématique, y compris des termes comme « impossible », « peu probable », « équiprobable », « très probable » et « certain » pour exprimer la probabilité que des événements se produisent et s’appuyer sur cette probabilité pour faire des prédictions et prendre des décisions éclairées.

HABILETÉ : UTILISER LE VOCABULAIRE MATHÉMATIQUE POUR EXPRIMER LA PROBABILITÉ QU’UN ÉVÉNEMENT SE PRODUISE

Chez les élèves, au cycle primaire, la pensée probabiliste se développe quotidiennement grâce à l’apprentissage de certains mots ou expressions qui permettent de décrire la fréquence ou la probabilité de certains événements (par exemple, Nous avons toujours congé d’école le samedi et le dimanche. C’est possible que je joue au ballon à la récréation. Il est peu probable qu’il pleuve aujourd’hui.). Les élèves développent aussi une compréhension des concepts de variabilité et de hasard en réalisant des expériences simples de probabilité. Même si leur compréhension de la probabilité théorique est toujours à l’état embryonnaire, elles et ils peuvent reconnaître, par exemple, qu’en faisant tourner l’aiguille d’une roulette séparée en tiers, il y a 1 possibilité sur 3 que l’aiguille s’arrête sur le tiers qui est rouge.

Un diagramme circulaire muni d’une aiguille est séparé en trois parties égales de différentes couleurs : une violette, une rouge et une jaune. L’aiguille pointe dans le secteur jaune.

Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 128.

Au cycle primaire, une des premières manifestations du sens de la variabilité survient lorsque les élèves sont en mesure d’indiquer s’il est certain, possible ou impossible qu’un événement donné se produise (par exemple, C’est impossible que les vaches se mettent à voler). Certaines et certains jeunes élèves éprouvent beaucoup de difficulté à le faire. Pour plusieurs, ce qui est possible devient certain. Par exemple, si le personnel enseignant leur dit qu’il est possible qu’il amène son chien en classe le lendemain, ces élèves seront très déçues et déçus s'il ne le fait pas puisque dans leur esprit, c’est certain qu’il va l’amener. Les élèves doivent comprendre que si un événement est possible, il peut tout aussi bien se produire que ne pas se produire. D’autres élèves ont de la difficulté à faire la distinction entre ce qui ne s’est jamais produit et ce qui ne peut jamais se produire. Pour elles et eux, si un événement ne s’est jamais produit, c’est qu’il est impossible. Par exemple, elles et ils peuvent penser que c’est impossible de passer toute une nuit sans dormir parce qu’elles et ils ne l’ont jamais fait. Par contre, un tel événement n’est pas impossible pour autant.

Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 132-133.

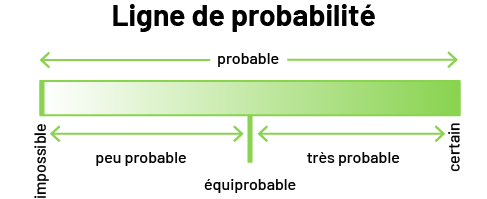
La notion de probabilité peut être représentée sur un continuum allant de impossible à certain, chaque terme qualifiant le degré de probabilité : impossible, peu probable, équiprobable, très probable et certain.

HABILETÉ : FAIRE DES PRÉDICTIONS ET PRENDRE DES DÉCISIONS ÉCLAIRÉES

En Données, la démarche de résolution de problèmes préconisée fait appel au processus d’enquête. Cette démarche favorise l’acquisition d’une pensée probabiliste critique en incitant les élèves à formuler des conclusions à partir de données recueillies lors d’expériences de probabilité et à remettre en question leur intuition en ce qui a trait à la probabilité d’un des résultats. Une telle approche permet d’éviter le développement de certaines des fausses conceptions de probabilité que l’on retrouve trop souvent tant chez les élèves que chez les adultes.

Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 128.

C’est uniquement par l’expérience et la discussion avec leurs pairs qu’elles et ils (les élèves) finiront par comprendre que le hasard n’a pas de mémoire. Pourtant, beaucoup d’adultes n’arrivent pas à en prendre conscience.

(Van de Walle et Lovin, 2008, p. 363.)

Une connaissance des concepts liés à la probabilité aide les élèves à mieux comprendre toutes sortes de situations de la vie de tous les jours (par exemple, compréhension des prévisions météorologiques, des résultats possibles d’une expérience, de la probabilité de gagner lors d’un tirage ou d’un jeu). La grande idée Probabilité met l’accent sur l’importance de la pensée probabiliste pour éclairer la prise de décision dans des situations dont l’issue est incertaine en raison du fait qu’elle est liée au hasard.

Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 127.

Concept de probabilité

La probabilité permet de décrire, dans une situation de variabilité, le niveau de certitude avec lequel on peut prédire que tel résultat ou tel événement aura lieu. Développer une bonne compréhension du concept de probabilité est un long processus qui s’amorce dès les premières années d’études. Il est toutefois très important de d’abord miser sur une compréhension intuitive de ce concept. Au cycle primaire, les élèves sont en mesure de reconnaître intuitivement que dans une situation donnée, certains événements sont possibles et que le niveau de certitude qu’ils se produisent se situe sur un continuum qui va de impossible à certain. Le modèle de la ligne de certitude est un moyen visuel efficace pour décrire ce continuum.

Sous le titre « Ligne de certitude », le mot « possible » apparaît entre deux flèches pointant vers les extrêmes de la barre progressive qui se trouve en dessous. Celle-ci commence avec la couleur blanche et devient graduellement bleue. À l’extrême-gauche, on trouve le mot « impossible », et à l’extrême-droite on trouve le mot « certain ».

Les élèves situent de façon approximative un point sur ce continuum pour décrire dans quelle mesure elles et ils sont certaines et certains qu’un événement donné va se produire. Plus elles et ils le situent vers la droite de la ligne, plus leur niveau de certitude est élevé. Si elles et ils le situent au centre, c’est qu’elles et ils estiment que l’événement est aussi probable de se produire que de ne pas se produire.

Vers la fin du cycle primaire, les élèves commencent à remplacer le mot possible par le mot probable. Elles et ils peuvent alors qualifier un événement de peu probable ou de très probable (par exemple, Il est peu probable qu’il pleuve aujourd’hui.) et le représenter par un point sur une ligne de probabilité. En 3e année, les élèves développent leur compréhension du concept de probabilité en utilisant les termes impossible, peu probable, équiprobable, très probable et certain afin de situer des événements sur une ligne de probabilité. À ce stade de développement du concept de probabilité, il n’est toujours pas question de quantifier la probabilité de façon précise. Les événements sont donc situés de façon approximative sur la droite.

Sous le titre « Ligne de probabilité », le mot « probable » apparaît entre deux flèches pointant vers les extrêmes de la barre progressive qui se trouve en dessous. Celle-ci commence avec la couleur blanche et devient graduellement verte. À l’extrême-gauche, on trouve le mot « impossible », à l’extrême-droite on trouve le mot « certain », et en plein centre on trouve le mot « équiprobable ». Entre « impossible » et « équiprobable », qui sont reliés par une flèche double sens, on trouve l’expression « peu probable ». Entre « équiprobable » et « certain », qui sont reliés par une flèche double sens, on trouve l’expression « très probable ».

Les élèves commencent aussi à porter une attention plus particulière aux résultats possibles d’une situation donnée. Le personnel enseignant doit donc leur présenter des situations simples qui font appel à du matériel concret et qui les incitent à énumérer ces résultats et à comparer leur probabilité.

Exemple

Le personnel enseignant présente aux élèves les trois roulettes ci-dessous et leur demande de comparer la probabilité de certains des résultats.

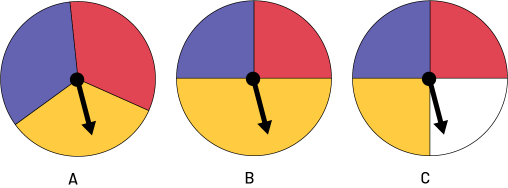
Trois roulettes munies d’une aiguille sont placées côte à côte. La roulette A est séparée en trois parties égales de différentes couleurs : une violette, une rouge et une jaune. L’aiguille pointe dans la partie jaune. La roulette B est séparée en trois parties : la partie jaune prend la moitié, tandis que la partie rouge et la partie violette prennent chacune un quart. L’aiguille pointe dans la partie jaune. La roulette C est séparée en 4 parties égales : rouge, violette, jaune et blanche. L’aiguille pointe dans la partie blanche.

Voici quelques réponses possibles :

  • Avec la roulette B, il est plus probable d’obtenir le résultat jaune que d’obtenir le résultat bleu ou le résultat rouge.
  • Avec la roulette A, les résultats bleu, rouge et jaune sont équiprobables.
  • Avec la roulette C, les quatre résultats sont aussi équiprobables.
  • Il est plus probable d’obtenir le résultat rouge avec la roulette A qu’avec la roulette C.

Le personnel enseignant peut profiter de cette situation pour inciter les élèves à réfléchir à la notion de résultats équiprobables, une notion fondamentale pour le développement d’une compréhension de la probabilité théorique. Il peut faire ressortir le fait que les roulettes A et B ont chacune trois résultats possibles (rouge, bleu et jaune) et leur demander d’expliquer pourquoi les résultats de la roulette A sont équiprobables et pas ceux de la roulette B. Ce type de questionnement permet au personnel enseignant d’aider les élèves à comprendre l’importance de toujours remettre en question leur intuition et de bien réfléchir lorsqu’elles et ils analysent une situation.

Le personnel enseignant peut ensuite demander aux élèves d’effectuer, en équipe, une petite expérience de probabilité qui consiste à faire tourner chaque roulette un certain nombre de fois (par exemple, 100 fois) et à noter les résultats. Puis, il leur demande de vérifier si les résultats obtenus appuient les réponses données préalablement. Le personnel enseignant mise sur la variabilité des résultats obtenus par les différentes équipes pour souligner de nouveau le fait que dans toute situation de probabilité, les résultats sont aléatoires et qu’elles et ils ne peuvent être déterminés avec certitude.

Les expériences de probabilité permettent d’appuyer ou de remettre en question un raisonnement intuitif; elles sont au cœur du développement de la pensée probabiliste.

Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 134-136.

Au fur et à mesure que les élèves acquièrent de l’expérience dans la résolution de situations de variabilité, certaines et certains ont tendance à développer de fausses conceptions. L’une des fausses conceptions les plus répandues a trait à l’imposition de limites implicites à la variabilité. Par exemple, au jeu de pile ou face, les élèves obtiennent le côté pile cinq fois de suite. Si on leur demande alors de prédire le résultat du prochain lancer, plusieurs auront tendance à indiquer qu’il correspondra certainement au côté face parce que leur intuition les porte à croire qu’il y a une limite à ce que le hasard favorise le côté pile. Le personnel enseignant doit les aider à comprendre que le hasard n’a pas de mémoire, c’est-à-dire que chaque résultat est indépendant des résultats précédents et qu’il est impossible de le prédire avec certitude. Il est donc tout aussi probable d’obtenir le côté pile que d’obtenir le côté face au prochain lancer. Ce genre de méprise persiste chez de nombreux adultes qui croient, par exemple, que certains numéros ont de meilleures chances de faire partie des numéros gagnants à la loterie pour la simple raison qu’ils sont sortis plus souvent dans le passé. Une bonne compréhension du concept de variabilité permet de reconnaître qu’il n’en est rien. Pour aider les élèves à bien saisir ce concept, le personnel enseignant doit leur présenter de nombreuses expériences simples de probabilité et les inciter à se questionner et à demeurer objectifs à l’égard de leur intuition.

Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 133-134.