C1.2 Créer des suites à motif répété, des suites croissantes et des suites décroissantes comprenant des nombres naturels et des nombres décimaux à l’aide d’une variété de représentations, y compris des expressions algébriques et des équations pour des suites croissantes linéaires, et établir des liens entre les différentes représentations.
Habileté : créer diverses suites
Avant de créer des suites, les élèves doivent d’abord reconnaître, comparer, décrire, changer la représentation et prolonger une grande variété de suites. Les élèves démontrent leur compréhension du concept de règle en créant une suite et en l’expliquant.
Au départ, l’utilisation du matériel de manipulation est indispensable pour représenter les suites. En effet, au moment de la création de suites, les élèves peuvent facilement changer un élément du motif et vérifier la régularité. Par contre, en dessinant une suite sur du papier, les élèves se concentrent sur le dessin à reproduire plutôt que sur la suite entière ou la nature de la règle.
Au début, le personnel enseignant fait travailler les élèves en petits groupes afin de favoriser l’échange d’idées, et peut fournir les attributs et la structure de la suite ainsi que le matériel nécessaire pour la créer.
Au cours d’un échange mathématique, les présentations des suites permettent de déterminer les différentes représentations d’une même règle et de vérifier la façon dont les élèves communiquent leur compréhension.
Ensuite, le personnel enseignant peut demander aux élèves de créer chacune et chacun une suite et de l’échanger avec une ou un partenaire. Les élèves peuvent alors créer une représentation différente de la suite reçue, décrire sa structure, la prolonger ou en produire une complètement différente aux fins de comparaison. Il faut cependant limiter le nombre d’éléments dans le motif, car certaines et certains élèves en utilisent trop, ce qui rend difficile l’identification de la structure de la suite.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 39-40.
Exemple
Donner une règle de régularité d’addition ou de soustraction (par exemple, +23 ou -23). Demander aux élèves de créer différentes suites ayant la même règle de régularité et de les comparer.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 63.
Habileté : représenter des suites et établir des liens entre les différentes représentations
L’habileté à communiquer un raisonnement algébrique se développe lorsque les élèves expriment leur compréhension d’une situation-problème ou d’un concept, et défendent leurs idées en utilisant différents modes de représentation :
- concret, lié à l’exploration, à la manipulation et à la création à l’aide de matériel concret;
- semi-concret, lié à une illustration, à un dessin ou à toute autre représentation sur papier;
- symbolique, lié à toute représentation faite à partir de chiffres ou de symboles;
- « en mots », lié à une explication ou à une description verbale ou écrite.

Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 18.
Afin d’acquérir une solide compréhension, les élèves doivent vivre des expériences en contexte en explorant des situations-problèmes. La mise en contexte permet aux élèves d’établir des liens entre diverses représentations et de développer une compréhension des concepts algébriques explorés. Le personnel enseignant utilise aussi diverses représentations afin d’aider les élèves à s’approprier les concepts mathématiques, à établir des liens entre les représentations, à faciliter le transfert et à provoquer une flexibilité cognitive en lien avec les concepts.
Les élèves explorent les relations et les représentent de différentes façons. Les élèves apprennent qu’une relation peut être représentée par une situation (suite non numérique), une table de valeurs, une expression algébrique, une équation (règle) ou une représentation graphique. Les flèches dans le schéma ci-dessous indiquent les liens entre les diverses représentations usuelles d’une relation.
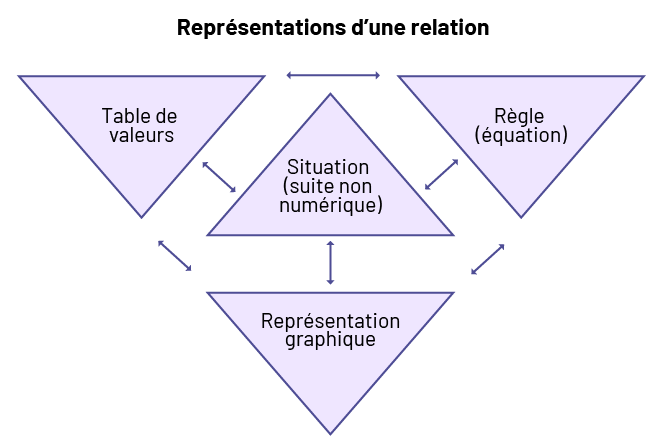
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 41.
L’utilisation de représentations multiples d’une même suite pour communiquer sa compréhension est une composante essentielle du développement de la pensée algébrique. Les suites à motif répété, les suites croissantes et les suites décroissantes peuvent être représentées sous différentes formes, soit à l’aide de matériel concret, de représentations graphiques, de tables de valeurs, d’équations, d’expressions algébriques et de description orale.
Description orale
Représenter une suite à motif répété à l’aide de mots
Cette suite est une suite à motif répété. Son motif de base est 4 triangles rouges et deux carrés bleus, et ce motif est répété toujours dans le même ordre. Les attributs de la suite sont les formes et les couleurs. Sa structure est AAAABB.

Représenter une suite croissante à l’aide de mots
Lorsqu’une suite croissante est présentée aux élèves, le personnel enseignant doit leur offrir différentes occasions de la décrire à l’aide de mots. Il s’agit d’une étape essentielle dans le cheminement des élèves pour les amener à déterminer l’expression algébrique de la suite.
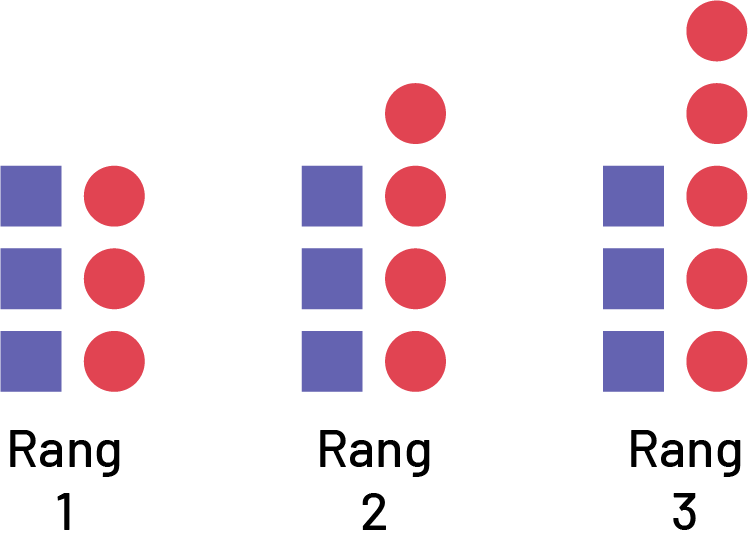
La suite croissante peut être décrite comme suit :
Au 1er rang, la figure est composée de 3 carrés bleus et de 3 cercles rouges.
Au 2e rang, la figure est composée de 3 carrés bleus et de 4 cercles rouges.
Au 3e rang, la figure est composée de 3 carrés bleus et de 5 cercles rouges.
Les élèves peuvent aussi remarquer que le nombre de carrés bleus, soit 3, demeure constant, tandis que le nombre de cercles rouges augmente de 1.
Matériel de manipulation
Le matériel de manipulation (par exemple, carreaux algébriques, cubes emboîtables, jetons, réglettes Cuisenaire) est très varié. Son utilisation aide les élèves à explorer, à représenter et à faire des modifications facilement en cours d’essais. Voici des exemples d’utilisation de matériel de manipulation.
Représenter une équation à l’aide de matériel de manipulation
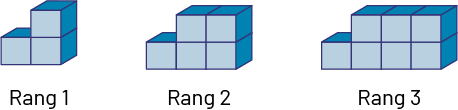
Le personnel enseignant peut donner l’équation ci-dessous aux élèves et leur demander de la représenter à l’aide de cubes emboîtables.
\(c = 1 + 2r\)
Exemple de raisonnement d’élève:
- Verbaliser la relation : Pour déterminer le nombre de cubes dans une figure, je commence par 1 et j’ajoute le rang de la figure multiplié par 2.
- Visualiser la relation :
Dans la figure au 1er rang, j’ai 1 cube et 1 groupe de 2 cubes.
Dans la figure au 2e rang, j’ai 1 cube et 2 groupes de 2 cubes.
Dans la figure au 3e rang, j’ai 1 cube et 3 groupes de 2 cubes.
Illustration
L’illustration permet aux élèves de créer une représentation personnelle semi-concrète de leurs observations et de leur compréhension, ce qui les aide à clarifier leur pensée. Elle s’avère particulièrement avantageuse pour les élèves qui éprouvent de la difficulté à écrire ou à utiliser des symboles comme moyen de représentation, les dessins tenant lieu de justifications ou d’explications.
De nombreux types de problèmes incitent naturellement les élèves à réaliser un dessin pour les aider à les résoudre. Il arrive aussi qu’elles et ils aient recours au matériel de manipulation en même temps. Or, plus les élèves acquièrent une pensée abstraite, plus elles et ils délaissent le matériel de manipulation pour des dessins. Voici des exemples d’utilisation d’une illustration.
Représenter une suite croissante au moyen d’une illustration
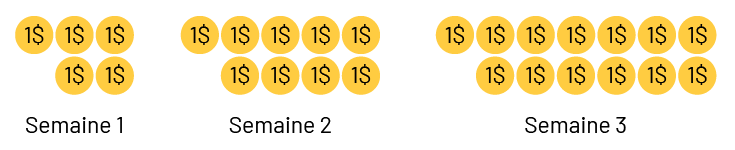
Simon veut se procurer un jouet, mais il n’a pas assez d’argent dans sa tirelire. Ses parents décident de lui remettre chaque semaine une même somme d’argent qu’il dépose dans sa tirelire. Afin de tenir compte de la somme accumulée dans sa tirelire, Simon a créé la table de valeurs suivante :
| Nombre de semaines | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Somme dans la tirelire | 5 | 9 | 13 | 17 |
Demander aux élèves d’illustrer la situation et de déterminer la somme d’argent que les parents lui donnent chaque semaine, et la somme accumulée de semaine en semaine.
Questions pertinentes
- De quelle façon l’illustration aide-t-elle à déterminer la règle?
- Quelle somme d’argent Simon aura-t-il dans la tirelire la 5e semaine? Comment le savez-vous?
- Si Simon reçoit une même somme chaque semaine, comment expliquer qu’il a 5 $ après la 1re semaine?
- Comment pouvez-vous déterminer la somme d’argent dans la tirelire après un grand nombre de semaines, par exemple, après la 10e semaine?
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 212-215.
Table de valeurs
La table de valeurs permet de représenter semi-concrètement la relation entre deux quantités changeantes (variables), dont l’une dépend de l’autre. La table de valeurs est souvent créée pour représenter la relation entre des valeurs numériques associées aux termes d’une suite non numérique croissante et le rang de ces termes.
La table de valeurs peut également être utilisée pour présenter des valeurs de variables d’une équation ou dans un contexte de résolution de problèmes.
Représenter une situation-problème à l’aide d’une table de valeurs
Dans un contexte de résolution de problèmes, les élèves peuvent aussi établir un lien entre une situation exprimée en mots et une table de valeurs.
Présenter la situation-problème suivante.
Un nouveau site Web de visionnement de films, Film Plus, est disponible. On doit payer un abonnement de 4 $ dès le visionnement du premier film. Donc, si on inclut le coût de l’abonnement, après avoir visionné successivement 1 film, 2 films, 3 films et 4 films, on aura déboursé 9 $, 14 $, 19 $ et 24 $.
Pour mieux comprendre cette relation, les élèves peuvent la modéliser en utilisant du matériel concret ou semi-concret et des mots.

|
Lorsqu’on visionne 1 film, il y a 4 $ d’abonnement et 1 x 5 $, donc on débourse 9$. Lorsqu’on visionne 2 films, il y a 4 $ d’abonnement et 2 x 5 $, donc on débourse 14$. Lorsqu’on visionne 3 films, il y a 4 $ d’abonnement et 3 x 5 $, donc on débourse 19$. Lorsqu’on visionne 4 films, il y a 4 $ d’abonnement et 4 x 5 $, donc on débourse 24$. |
Par la suite, les élèves peuvent utiliser une table de valeurs pour représenter la relation entre le nombre de films visionnés et la somme déboursée.
| Nombre de films visionnés | Montant déboursé ($) |
|---|---|
| 1 | 9 |
| 2 | 14 |
| 3 | 19 |
| 4 | 24 |
| ... | ... |
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 51.
Représenter une équation à l’aide d’une table de valeurs
Présenter l’équation \(g + k = 11\) et demander aux élèves de déterminer les valeurs entières possibles de g et de k.
| g | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Questions pertinentes
- Si g prend la valeur de 10, quelle valeur la variable k doit-elle prendre?
- Si k prend la valeur de 8, quelle valeur la variable g doit-elle prendre?
- Y a-t-il d’autres valeurs possibles? Comment pouvez-vous le vérifier?
- Comment pouvez-vous organiser les différentes possibilités dans une table de valeurs?
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 232-233.
Représentation graphique d’une relation
Un diagramme permet de représenter de façon schématique un ensemble de données. Au cycle moyen, au domaine Données, les élèves apprennent notamment à représenter des données en utilisant différents diagrammes. Les élèves peuvent se servir de ces connaissances dans le domaine Algèbre. L’allure de l’ensemble des données dans un diagramme (par exemple, bandes en ordre croissant ou décroissant) permet une analyse du changement et facilite l’interpolation et l’extrapolation. La table de valeurs est utilisée pour créer le diagramme. Voici des exemples d’utilisation d’un diagramme.
Représenter la relation entre deux quantités changeantes (dans une table de valeurs) à l’aide d’une représentation graphique
Présenter la situation suivante.
Samedi dernier, pendant le marathon, Louis et Gaëlle ont vendu de la limonade. À chaque pichet vendu, ils comptaient l’argent reçu. La table de valeurs ci-dessous représente la relation entre le nombre de pichets vendus et la somme perçue.
| Nombre de pichets vendus | 1 | 2 | 3 |
|---|---|---|---|
| Somme perçue ($) | 4 | 8 | 12 |
Ensuite, représenter les données dans un diagramme comme celui-ci :

Questions pertinentes
- Quels changements y a-t-il d’un pichet à l’autre en ce qui a trait à la vente? Ces changements sont-ils toujours les mêmes? Pourquoi?
- En examinant le diagramme, comment est-ce possible de déterminer la prochaine entrée d’argent?
- Quelle est la relation entre le nombre de pichets vendus et la somme perçue?
- Comment les trois premières valeurs représentées dans le diagramme peuvent-elles vous aider à déterminer la somme perçue après la vente de 8 pichets?
- Combien de pichets devaient-ils vendre pour obtenir une somme d’environ 50 $?
Dans cette vidéo, des élèves déterminent la règle pour créer une suite croissante linéaire. Les élèves utilisent une représentation de leur choix.
 Description de la vidéo
Description de la vidéo
Description à venir
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 233-234.
Habileté : représenter des suites croissantes linéaires à l’aide d’équations ou d’expressions algébriques
La progression des apprentissages décrite précédemment et reflétée dans les contenus d’apprentissage du programme-cadre de mathématiques ainsi que des recherches, notamment celle de Lee (1996, p. 105), suggèrent trois étapes qui mènent à la représentation d’une suite non numérique croissante à l’aide d’une règle :
- Visualiser la relation : percevoir les figures d’une certaine façon et reconnaître un lien entre elles.
- Verbaliser la relation : utiliser ce qui a été perçu afin d’énoncer une règle en langage courant.
- Représenter la relation à l’aide de symboles : exprimer la règle au moyen d’une équation composée de variables.
On peut illustrer ces trois étapes qui mènent à l’élaboration d’une équation à l’aide de la suite non numérique ci-dessous où l’on explore la relation entre le rang de la figure et le nombre de cubes qui la composent (règle de correspondance).

Raisonnement possible de l’élève
- Visualiser la relation :
Au 1er rang, je vois 1 cube et 1 groupe de 2 cubes.
Au 2e rang, je vois 1 cube et 2 groupes de 2 cubes.
Au 3e rang, je vois 1 cube et 3 groupes de 2 cubes.
Donc, au 10e rang, il y aura 1 cube et 10 groupes de 2 cubes.
- Verbaliser la relation : Pour déterminer le nombre de cubes à un rang donné, je commence par 1 et j’ajoute le rang multiplié par 2.
- Représenter la relation à l’aide de symboles : La relation peut être représentée par l’équation \(\ c = 1 + r \times 2\) où r représente le rang et c, le nombre de cubes qui la composent.
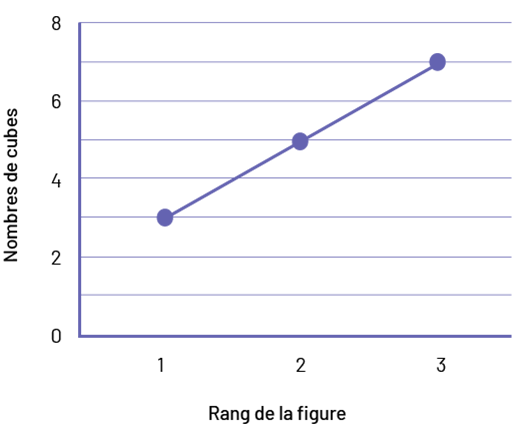
Cette relation peut être confirmée en créant une table de valeurs ainsi qu’une représentation graphique de la suite linéaire croissante.
| Rang de la figure ( r ) | Nombre de cubes ( c ) |
|---|---|
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| r | 1 + 2c |
Note : En 6e année, les élèves ont appris à effectuer des opérations arithmétiques en respectant la priorité des opérations. Les équations présentées dans ce document pour exprimer une règle tiennent compte de cette connaissance.
Il est important de reconnaître que ce cheminement vers l’expression d’une équation peut différer d’une ou d’un élève à l’autre, puisque le raisonnement se développe à partir de perceptions individuelles. L’exemple ci-dessous, inspiré d’une recherche de Radford (2006, p. 2-21), illustre comment des élèves peuvent percevoir différemment la relation entre le rang de la figure dans une suite non numérique croissante et le nombre de cercles qui composent chaque terme.
Exemple

L’élève 1 voit 2 rangées de cercles. Dans la rangée supérieure, il y a toujours 1 cercle de plus (en bleu) que le rang de la figure et, dans la rangée du bas, il y a toujours 2 cercles de plus (en gris) que le rang de la figure.
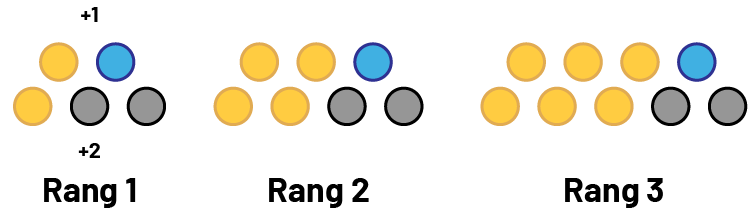
En poursuivant son analyse, l’élève détermine que la figure au 10e rang contiendra \((10 + 1) + (10 + 2)\) cercles, soit 23 cercles. L’élève conclut alors que la relation peut être représentée par l’équation \(c = (r + 1) + (r + 2)\), où r est le rang et c, le nombre de cercles qui la composent.
L’élève 2 trouve le nombre total de cercles en additionnant deux fois le rang et en ajoutant 3. Donc, pour le total de cercles au 1er rang, la phrase mathématique est \(1 + 1 + 3 = 5\); pour celle au 2e rang, \(2 + 2 + 3 = 7\) et pour celle au 3e rang, \(3 + 3 + 3 = 9\).

En poursuivant son analyse, l’élève conclut que la relation peut être représentée par l’équation \(c = r + r + 3\), où r est le rang et c, le nombre de cercles qui composent chaque terme.
L’élève 3 voit :
- au 1er rang, 5 cercles;
- au 2e rang, les 5 cercles initiaux, auxquels on a ajouté 1 groupe de 2 cercles;
- au 3e rang, les 5 cercles initiaux, auxquels on a ajouté 2 groupes de 2 cercles.

En analysant ces observations, l’élève généralise et constate qu’à chaque rang, il y a 5 cercles et un certain nombre de groupes de 2 cercles, ce nombre correspondant au rang précédent. Ainsi, au 25e rang, il y aura \(5 + 24 \times 2\) cercles, soit 53 cercles.
Note : L’élève peut présenter son interprétation à l’aide d’un tableau.
| Rang | Nombre de cercles | Explication à l'aide de la règle de régularité | Relation entre le rang et le nombre de cercles qui composent chaque terme (règle de correspondance) |
|---|---|---|---|
| 1 | 5 | 5 | 5+0x2 |
| 2 | 7 | 5+2 | 5+1x2 |
| 3 | 9 | 5+2+2 | 5+2x2 |
| 4 | 11 | 5+2+2+2 | 5+3x2 |
| 25 | ? | 5+2+2+2+... | 5+24x2 |
| r | 5+(r-1)x2 |
L’élève conclut que la relation peut être représentée par l’équation \(c = 5 + (r –1) \times 2\), où r est le rang et c, le nombre de cercles qui composent chaque terme.
Note : L’élève a analysé la relation en se basant sur la règle de régularité (soit l’ajout de 2 cercles à la figure précédente), ce qui la ou le mène vers la règle de correspondance en utilisant l’expression \(r – 1\) pour représenter le rang précédent, les 5 cercles initiaux et un certain nombre de groupes de 2 cercles, soit \(5 + (r – 1) \times 2\).
Les règles de correspondance formulées par les trois élèves proviennent de leur compréhension de cette relation. Chaque élève a perçu et généralisé la situation à sa façon, ce qui a engendré trois équations différentes, mais équivalentes. Aucune n’est meilleure qu’une autre. Elles démontrent toutefois que l’interprétation que les élèves se font d’une relation a un effet sur la règle qu’elles et ils formulent. Il est important que le personnel enseignant encourage ces différentes formulations d’une règle de correspondance. Ce faisant, il aide les élèves à développer une meilleure compréhension des équations et des variables.
Parfois, des élèves passent trop rapidement de la suite non numérique à la table de valeurs correspondante. Par exemple, à partir de la suite non numérique de l’exemple ci-dessus, les élèves établissent immédiatement la table suivante.
| Rang de la figure (r) | 1 | 2 | 3 |
|---|---|---|---|
| Nombre de cercles (c) | 5 | 7 | 9 |
Les élèves procèdent ensuite par tâtonnements pour déterminer l’équation qui définit la relation, comme en font foi les explications des deux élèves ci-dessous. Dans chaque cas, il y a lieu de remettre en question la profondeur de la compréhension qu’ont ces élèves de l’équation obtenue et de la relation qu’elle représente.
L’élève 4 explique qu’elle a représenté la relation à l’aide d’une table de valeurs. Elle a comparé le rang au nombre de cercles correspondant en faisant plusieurs essais. Par exemple, elle a commencé avec « × 2 », mais ça ne fonctionnait pas; ensuite elle a essayé « × 3 », mais ça ne fonctionnait pas non plus. Elle a continué de cette façon et a trouvé que dans chaque cas, c’était « fois deux plus trois » ou le double du rang, plus 3.
L’élève conclut que la relation peut être représentée par l’équation \(c = r \times 2 + 3\), où r est le rang et c, le nombre de cercles qui composent chaque terme.
L’élève 5 explique que dans la 2e ligne, il y a une régularité, car d’un terme à l’autre, on ajoute 2. Dans la règle, il y a donc « × 2 ». Elle ou il essaie la règle r × 2 et elle ou il n’obtient pas les termes 5, 7, 9… Elle ou il essaie alors la règle \(r \times 2 + 1\), puis la règle \(r \times 2 + 2\). Lorsqu’elle ou il essaie la règle \(r \times 2 + 3\), il obtient les termes 5, 7, 9…
L’élève conclut que la relation peut être représentée par l’équation \(c = r \times 2 + 3\), où r est le rang et c, le nombre de cercles qui composent chaque terme. Dans ce cas, cet élève semble déterminer l’équation en suivant une procédure apprise par cœur.
Le personnel enseignant doit tenir compte des façons différentes qu’ont les élèves de percevoir les relations entre les termes d’une suite, et adapter ses questions en conséquence afin d’aider chaque élève à exprimer la règle en mots avec précision et à déterminer l’équation qui lui correspond.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 53-57.
Représenter l’équation d’une suite croissante linéaire à l’aide d’une représentation semi-concrète
Il est aussi possible, par exemple, de représenter l’équation \(y = 2x + 4\) à l’aide de la suite non numérique croissante ci-dessous présentant les trois premières figures :

Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
La technologie
La technologie est un outil puissant pour observer et analyser les relations entre les variables. La calculatrice à affichage graphique et certaines applications Web sont utiles pour représenter, créer et analyser des données. Le graphique qui découle de l’entrée de données permet aux élèves d’observer si les données ont été entrées correctement, de déterminer la relation représentée et de modifier certaines données pour vérifier l’effet de ces changements sur le graphique. L’utilisation de la calculatrice à affichage graphique ou d’une application exigera l’apprentissage du fonctionnement de l’outil. Le temps dédié à l’apprivoisement de la technologie est réinvesti dans l’analyse des relations représentées par un graphique dans un diagramme. Les processus fondamentaux et les représentations de relations sont les composantes essentielles au développement des deux grandes idées du raisonnement algébrique.
Source : Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, p. 16.
Connaissance : table de valeurs
La table de valeurs permet de représenter semi-concrètement la relation entre deux quantités changeantes (variables), dont l’une dépend de l’autre. À la fin du cycle primaire, les élèves ont appris à créer des tables de valeurs pour représenter des relations dans des situations-problèmes.
La table de valeurs est souvent créée pour représenter la relation entre des valeurs numériques associées aux termes d’une suite non numérique croissante et le rang de ces termes.
Exemple
On peut étudier la relation entre le rang d’une figure dans une suite non numérique et le nombre d’objets qui composent le terme. Le rang est inscrit dans la première colonne (ou rangée) et le nombre d’objets qui composent la figure (valeur du terme) est inscrit dans la deuxième colonne (ou rangée). La règle de régularité des termes de la deuxième colonne (ou rangée) peut être utilisée pour prolonger la table de valeurs.
La table de valeurs peut être disposée verticalement ou horizontalement et séparée en colonnes ou en rangées. Il est bon de varier la présentation de la table de valeurs afin que les élèves s’habituent aux deux dispositions.
Table de valeurs à la verticale
| Rang de la figure | Nombre d’objets |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | … |
Table de valeurs à l’horizontale
| Rang de la figure | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Nombre d’objets | 2 | 4 | 6 | … |
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 231.
Connaissance : représentation graphique
Les suites non numériques croissantes peuvent servir d’introduction aux représentations graphiques. Le rang des figures dans les suites non numériques croissantes correspond aux valeurs sur l’axe horizontal. La valeur du terme de chaque figure est représenté par les valeurs sur l’axe vertical. L’axe vertical représente aussi la valeur du terme au rang 0 (la valeur de la constante), qui est l’ordonnée de la représentation graphique.
Source : Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, p. 63
Exemple
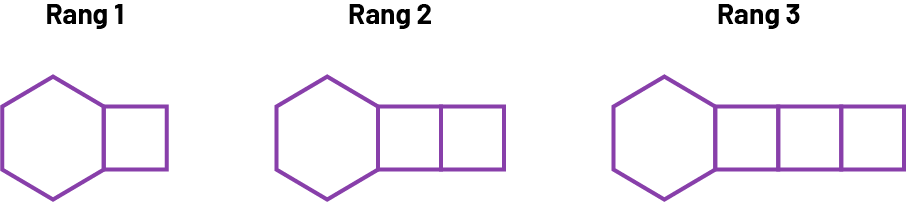
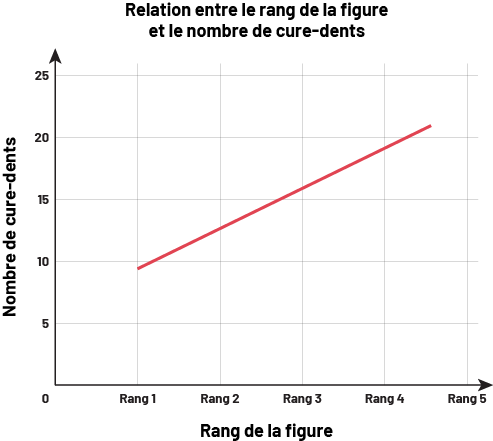
Source : En avant, les maths!, 6e année, CM, Algèbre, p. 5-6.
Connaissance : expression algébrique
Une expression algébrique est un symbole ou un ensemble de symboles qui peuvent être reliés entre eux à l’aide de symboles d’opérations.
Source: Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Note : Une expression contenant exclusivement des nombres est une expression numérique, par exemple 5 – 2.
Connaissance : équation
L’équation est une façon symbolique de représenter une relation qui peut être difficile à comprendre, entre autres, parce qu’il existe divers types d’équations dont la fonction varie selon la situation. Quatre types d’équations sont présentés aux élèves :
- Équation à résoudre : Une équation comme \(2 + n = 14\) doit être résolue. Elle provient généralement d’une situation-problème et décrit une relation d’égalité. La lettre n représente une valeur inconnue qui doit être déterminée.
- Équation qui représente une relation entre deux quantités changeantes : Une équation comme \(c = 2r + 3\) sert à exprimer une relation, par exemple la relation entre le numéro d’une figure (r) dans une suite non numérique et le nombre de cure-dents (c) qui la composent. Les lettres r et c sont des variables, puisqu’elles peuvent prendre diverses valeurs.
- Équation qui sert de formule : Pour calculer l’aire (A) d’un carré, on peut utiliser l’équation \(A = c \times c\). On appelle une telle équation une formule, puisqu’on l’utilise pour calculer l’aire d’un carré ayant des côtés de longueur c. On ne résout pas une telle équation.
- Équation qui généralise une situation d’égalité : On peut généraliser la relation d’égalité entre l’addition de deux nombres identiques quelconques et la multiplication de ce nombre par 2 (par exemple, \(4 + 4 = 2 \times 4\)) par l’équation \(n + n = 2 \times n\). On ne résout pas une telle équation et il ne s’agit pas d’une formule. De plus, elle ne représente pas une relation entre deux quantités changeantes.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 89.
