C1.1 Reconnaître et comparer une variété de suites à motif répété, de suites croissantes et de suites décroissantes, y compris des suites trouvées dans la vie quotidienne, et comparer les suites croissantes linéaires selon leurs taux constants et leurs valeurs initiales.
Habileté : reconnaître et comparer une variété de suites
Lorsque les élèves justifient leur raisonnement, c’est une occasion de prendre du recul et d’examiner leur démarche de façon logique.
Source : Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, p. 68.
Cela dit, la capacité des élèves à justifier les similitudes et les différences de certaines suites consolide leur apprentissage et développe leur habileté à communiquer. De plus, leur capacité à justifier deux suites qui sont semblables exige un degré de raisonnement plus élevé, et aide les élèves à miser sur les relations qui existent entre les suites.
La compréhension des relations est de toute première importance, car savoir reconnaître des relations deviendra ultérieurement une stratégie de résolution de problèmes. Pendant les échanges mathématiques, le personnel enseignant doit amener les élèves à comparer les caractéristiques particulières des suites telles que :
Pour les suites à motif répété :
- les attributs utilisés;
- le choix et la quantité d’éléments dans chaque motif;
- la structure de chaque suite;
- la règle de régularité dans chaque suite;
- la règle de correspondance dans chaque suite.
Pour les suites croissantes et décroissantes :
- ce qui change d’un terme à l’autre;
- ce qui est constant d’un terme à l’autre;
- la règle de régularité dans chaque suite;
- la règle de correspondance dans chaque suite.
L’habileté à comparer des suites facilite l’acquisition de l’habileté à les prolonger et, par la suite, à en créer de nouvelles. Pour amener les élèves à se créer une image mentale d’une règle, le personnel enseignant peut aussi faire comparer les suites en utilisant des exemples et des contre-exemples de suites. Cette stratégie permet aux élèves de reconnaître une suite, de trouver la règle de régularité ou la règle de correspondance, de la décrire et de justifier leur raisonnement tout en utilisant un vocabulaire mathématique approprié.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 33-34.
Des questions stratégiques du personnel enseignant viennent appuyer et renforcer l’habileté à comparer des suites.
Exemples de questions
- Pouvez-vous représenter ces suites différemment?
- Qu’observez-vous une fois que les deux suites sont représentées dans la table de valeurs? une fois sous forme de représentation graphique?
- Y a-t-il des éléments, des nombres qui font partie des deux suites?
- Quelle est la relation entre ces éléments, ces nombres?
- Quelle est la règle de régularité dans chaque suite?
- Quelle est la règle de correspondance dans chaque suite croissante?
- Quelle ressemblance et quelle différence y a-t-il entre les suites?
- Pouvez-vous représenter ces suites différemment? Expliquez ou démontrez votre réponse.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 59-60.
Exemple de comparaison de suites croissantes
D’abord, il est important de noter si l’on est en présence de suites croissantes ou décroissantes. Il est également très important de repérer le motif de base et la règle de régularité dans la croissance des termes.
Le schéma ci-dessous démontre que le nombre de conifères et de pommiers augmente, le premier de façon linéaire et, le second, de façon non linéaire.

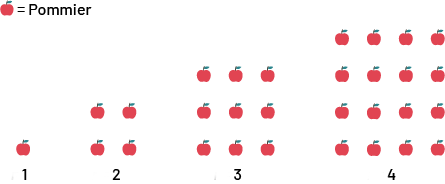
Cela peut être illustré à l’aide de tables de valeurs et de représentations graphiques.
- Table de valeurs
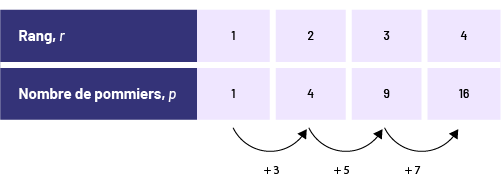
À partir d’une table de valeurs, une suite croissante peut être dite linéaire ou non en déterminant la règle de régularité (« +3, +5, +7 » illustré ci-dessus). Si les bonds ne sont pas constants, comme c’est le cas ici, la suite croissante est non linéaire.
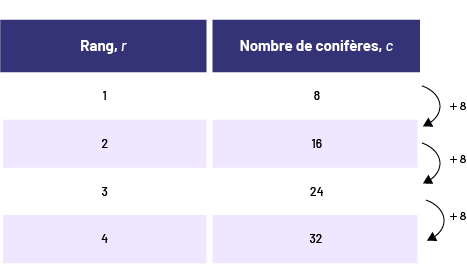
À partir d’une table de valeurs, une suite croissante peut être dite linéaire ou non en déterminant la règle de régularité (« +8, +8, +8 » illustré ci-dessus). Si les bonds sont constants, comme c’est le cas ici, la suite croissante est linéaire.
- Représentations graphiques
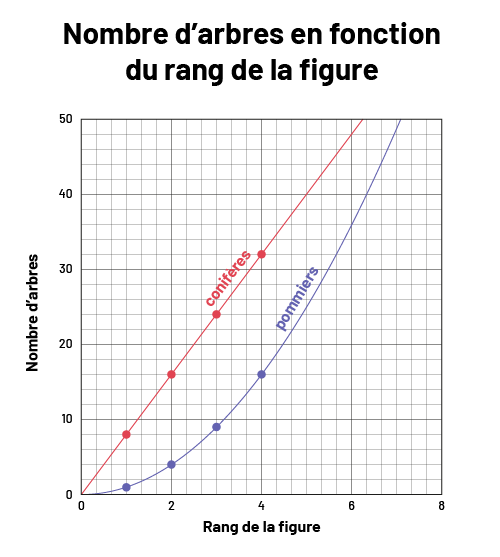
Dans ce cas, l’élève doit pouvoir noter que le nombre de pommiers, selon le rang, représente une suite croissante qui est non linéaire et commence à 0 pour le rang 0. Celle-ci est non linéaire, puisque le nombre de pommiers ne croît pas selon un taux constant. Dans la table de valeurs, lorsque le rang augmente de 1, le nombre de pommiers augmente de façon non constante. Elle produit une ligne courbe dans sa représentation graphique.
Le nombre de conifères commencerait également à 0. Dans la table de valeurs, chaque fois que le rang augmente de 1, le nombre de conifères augmente toujours de 8. Cette relation est donc une suite croissante linéaire, car elle augmente avec un taux de variation constant de 8 conifères par rang. Son équation est représentée par c = 8r. Son graphique représente une droite dans le plan cartésien.
Source : Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, p. 15-16.
Des relations décroissantes, tel le nombre de friandises restantes dans un contenant, peuvent être présentées de la même façon.
Habileté : comparer les suites croissantes linéaires selon leurs taux constants et leurs valeurs initiales
Lorsque l’on compare des suites croissantes linéaires, on compare leur taux constant ainsi que leur valeur initiale.
L’équation d’une suite linéaire est \( y = mx +b\) , dans laquelle m représente le taux de variation constant et \(b\) , la valeur initiale.
Si le rapport entre le changement d’une variable et le changement d’une autre variable est équivalent dans deux ensembles de données, alors il y a un taux constant. Un exemple d’application réelle d’un taux constant est un salaire de 15 $ l’heure.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1er à la 8e année, 2020, ministère de l’Éducation de l’Ontario.
Parmi des suites croissantes linéaires, celle avec le taux constant le plus élevé est celle qui croît le plus rapidement et dont la représentation graphique est la plus inclinée. Par exemple, cela est vrai pour un taux de variation constant \((m)\) de 3 comparativement à un taux de variation constant \((m)\) de 2.
Taux constant de 3 :
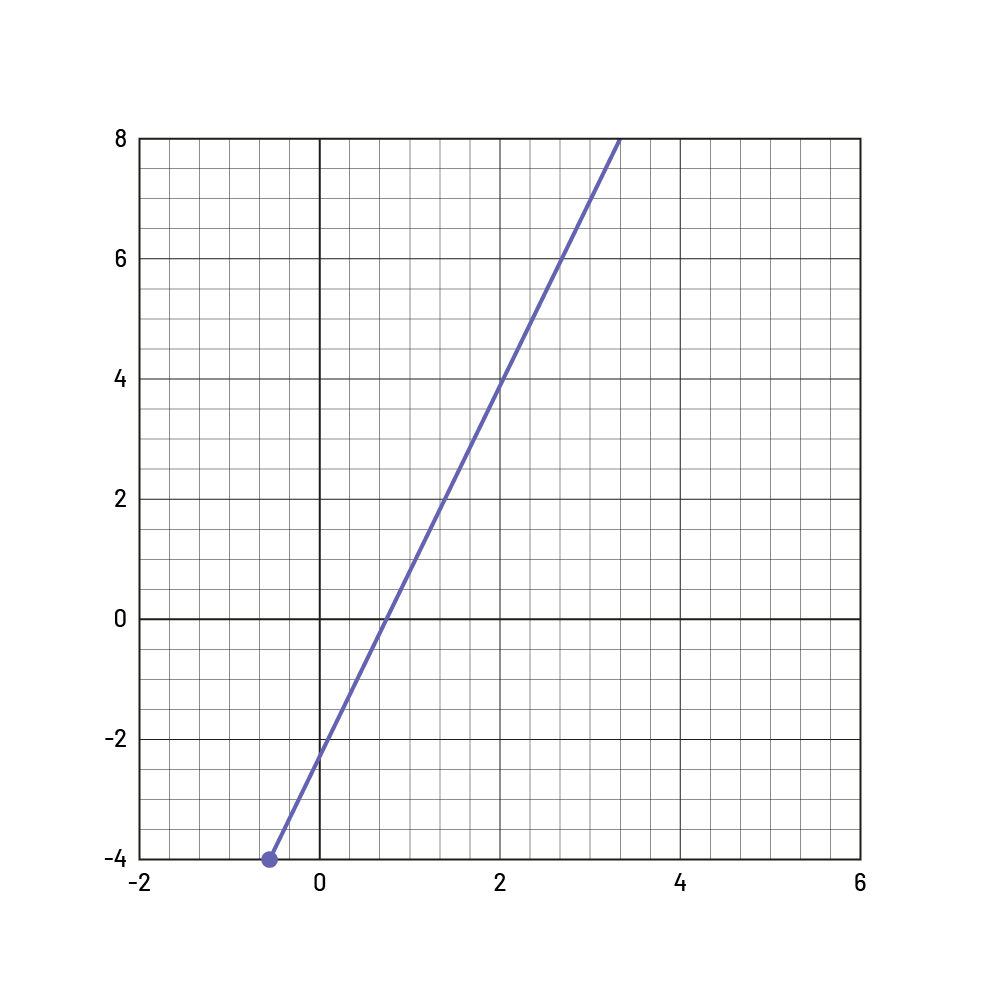
Taux constant de 2 :
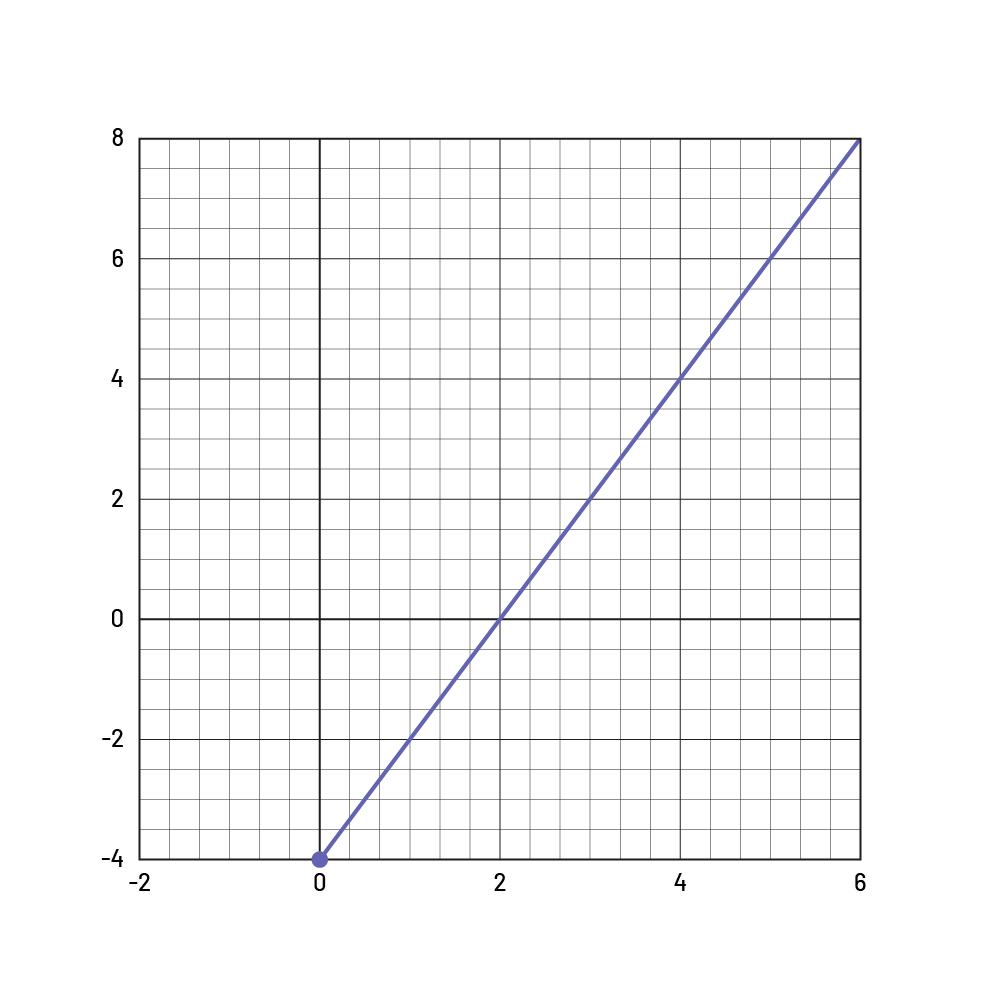
Source : En avant, les maths!, 7e année, CM, Algèbre, p. 5.
Lorsqu’on représente une suite linéaire graphiquement, la valeur initiale correspond à la valeur de y lorsque x vaut 0.
Exemple
La valeur initiale de la suite croissante linéaire \(y = 3x – 2\) est de \(-2\), puisque lorsque \(x = 0\), \(y = -2\).
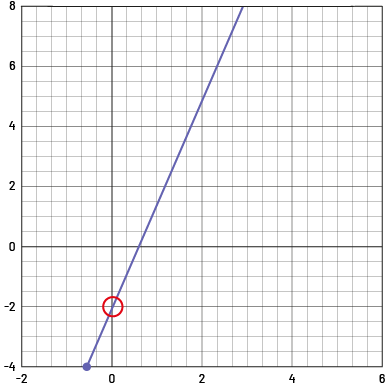
Il est à noter que le graphique d’une suite croissante linéaire qui a une valeur initiale de zéro passe par l’origine à \((0, 0)\).
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1er à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Connaissance : suite non numérique
Ensemble de figures ou d’objets disposés selon un ordre et une régularité.
Suite à motif répété
Ensemble de figures ou d’objets, disposés selon un ordre et une régularité, dans lequel on trouve un motif répété.
Exemple

Suite croissante
Ensemble de figures ou d’objets, disposés selon un ordre et une régularité, dans lequel on distingue un motif de base qui croît d’un terme à l’autre.
Exemples
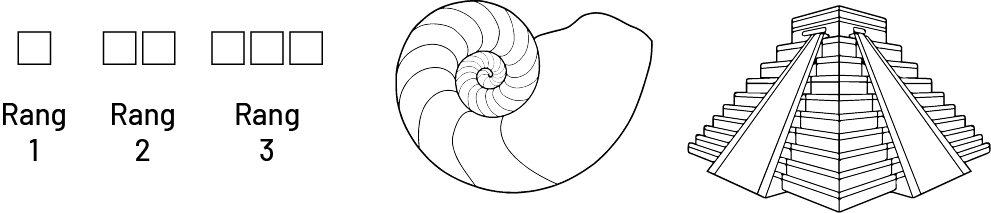
Le premier exemple représente une suite croissante; le motif de base est un carré auquel on ajoute un carré à chaque rang subséquent.
Le deuxième exemple représente un coquillage en spirale, dont le 1er terme (motif de base) est la première spirale au centre du coquillage. Les autres termes s’obtiennent selon une certaine régularité (souvent associée à la suite de Fibonacci et au nombre d’or). La suite que forment les différentes spirales est croissante, car la grosseur des spirales augmente selon une régularité.
Le dernier exemple représente une pyramide, dont le 1er terme est un prisme rectangulaire au sommet, auquel on ajoute des pierres dont l’aire de la base croît selon une certaine régularité.
Suite croissante linéaire
Suite qui augmente (croît) par une valeur qui reste constante. Dans un système de coordonnées, elle est représentée sous la forme d’une ligne droite.
Exemples
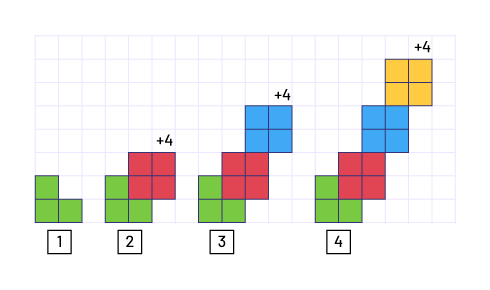
La suite ci-dessous commence par trois carrés au rang 1 (motif de base et valeur initiale) et chaque terme augmente de quatre carrés (bond constant) à chaque rang subséquent.
La suite ci-dessous commence par quatre carrés au rang 1 (motif de base et valeur initiale) et chaque terme augmente de trois carrés (bond constant) à chaque rang subséquent.
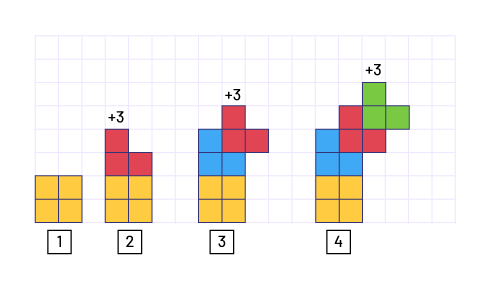
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Suite décroissante
Ensemble de figures ou d’objets, disposés selon un ordre et une régularité, qui implique une régression (par exemple, une diminution du nombre d’éléments) d’un terme à l’autre.
Exemple

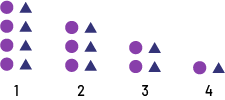
La suite ci-dessus commence par 4 cercles violets et 4 triangles bleus au rang 1, et chaque terme au rang subséquent diminue d’un triangle bleu de plus (-1, -2).
Suite décroissante linéaire
Suite dont la valeur des éléments, qui peut être représentée par y, diminue au fur et à mesure que le rang, représenté par x, augmente. Le taux de variation est constant, mais il a une valeur négative.
Connaissance : suite numérique
Suite numérique croissante : Suite où les termes sont des nombres qui croissent (augmentent). Les termes d’une suite croissante proviennent de règles de régularité liées à l’addition et à la multiplication.
Exemples
- 4, 6, 8, 10... (La règle de régularité de cette suite est d’additionner 2 afin d’obtenir le terme au rang subséquent.)
- 1, 2, 4, 7, 11… (La règle de régularité de cette suite est d’additionner 1 de plus que la fois précédente afin d’obtenir le terme au rang subséquent.)
- 3, 9, 27, 81… (La règle de régularité de cette suite est de multiplier par 3 afin d’obtenir le terme au rang subséquent.)
Suite numérique décroissante : Suite où les termes sont des nombres qui diminuent. Les termes d’une suite décroissante proviennent de règles de régularité liées à la soustraction et à la division.
Exemples
- 14, 11, 8… (La règle de régularité de cette suite est de soustraire 3 afin d’obtenir le terme au rang subséquent.)
- 144, 72, 36… (La règle de régularité de cette suite est de diviser par 2 afin d’obtenir le terme au rang subséquent.)
Connaissance : motif
La plus petite partie d’une suite non numérique à partir de laquelle la régularité est créée.
Suite à motif répété

Le motif est :

Suite non numérique croissante
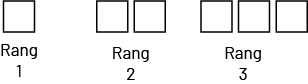
Le motif est:

En examinant les suites ci-dessus, on peut reconnaître qu’elles sont créées en fonction d’un motif qui se répète.
Connaissance : attribut
Propriété observable d’une personne ou d’un objet. Les attributs peuvent inclure la couleur, la forme, la texture, l’épaisseur, l’orientation, les matériaux, les mouvements, les sons, les objets ou les lettres. L’attribut d’un objet est représenté au moyen d’une caractéristique. Par exemple, si l’attribut est la couleur, les caractéristiques peuvent être rouge, bleu, jaune.
Dans la suite ci-dessous, les attributs qui décrivent la suite sont la forme et la couleur. Les caractéristiques de la forme sont : rectangle, trapèze et triangle. Les caractéristiques de la couleur sont : bleu, vert et orange.

Source : adapté du curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Connaissance : terme
Chaque figure, objet, mouvement qui compose une suite non numérique ou chaque nombre qui compose une suite numérique.
Suite à motif répété
Dans la suite ci-dessous, chacune des figures planes est un terme.


Suite non numérique croissante
Dans la suite, chacune des figures est un terme.

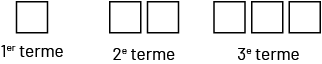
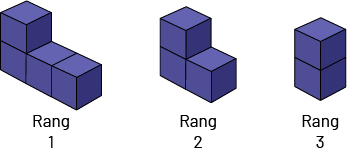
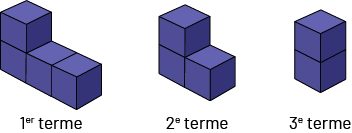
Suite non numérique décroissante
Dans la suite, chacune des figures est un terme.
Suite numérique croissante
2, 4, 6, 8… (1er terme : 2, 2e terme : 4, 3e terme, 6)
4, 10, 16, 22, 28... (1er terme : 4, 2e terme : 10, 3e terme : 16)
Suite numérique décroissante
21, 14, 7... (1er terme : 21, 2e terme : 14, 3e terme : 7)
72, 60, 48... (1er terme : 72, 2e terme : 60, 3e terme : 48)
Connaissance : règle de régularité
Règle qui permet de prolonger une suite en respectant la différence entre les termes (aussi appelé bond constant).
Exemple
Règle de régularité dans la suite : un cube est toujours ajouté à la rangée du bas du rang précédent.
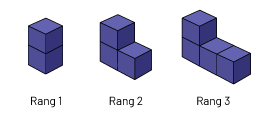
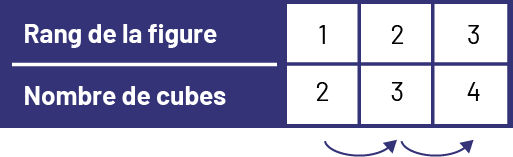
Connaissance : règle de correspondance
Règle qui permet de prolonger une suite en établissant la relation entre le rang et son terme.
Dans la suite ci-dessous, la règle de correspondance est la suivante : le nombre de triangles dans la figure correspond à 3 fois son rang.
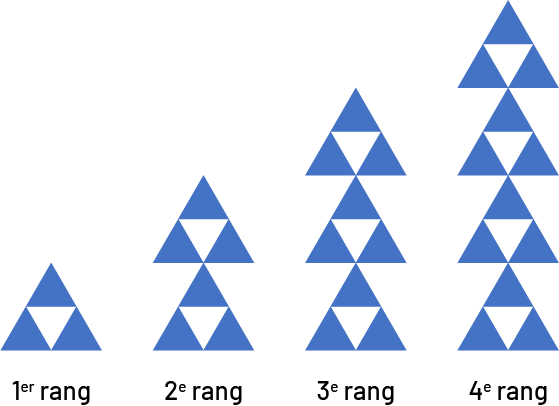
Le nombre de triangles \((t)\) est égal à trois fois le rang \((r)\), donc \(t = 3r\).
Dans cette prochaine suite, le triangle vert est constant d’un rang à l’autre et le nombre de groupes de 2 carrés orange correspond au rang de la figure.
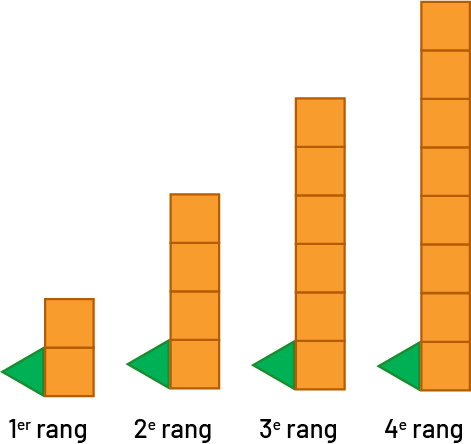
|
Au 1er rang, il y a 1 triangle vert et 1 groupe de 2 carrés orange. Au 2e rang, il y a 1 triangle vert et 2 groupes de 2 carrés orange. Au 3e rang, il y a 1 triangle vert et 3 groupes de 2 carrés orange. Au 4e rang, il y a 1 triangle vert et 4 groupes de 2 carrés orange. |
Le nombre de figures planes \((f)\) est égal à 2 fois le rang \((r)\) plus 1, donc \(f = 2r + 1\).
Connaissance : structure
Représentation à l’aide de lettres de la règle de régularité d’une suite à motif répété.
Dans la suite, chaque élément du motif peut être identifié par une lettre comme suit : rectangle bleu (A), trapèze vert (B), triangle orange (C). La structure de la suite A est donc ABC.

Connaissance : rang
Position qu’occupe chaque terme dans une suite. Le rang est indiqué par un nombre. Il est utilisé pour aider à décrire les relations dans une suite et à prédire les prochains termes dans la suite sans avoir à la prolonger.
Exemples
Dans les suites, chaque figure a son rang : la figure 1 occupe le 1er rang, la figure 2 occupe le 2e rang, etc.
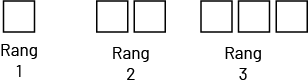

Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 29.
Connaissance : taux constant (ou taux de variation constant)
Pour deux paires de données quelconques, rapport équivalent entre le changement d’une variable et le changement d’une autre variable. Dans l’équation \( y = mx +b\) , le taux constant est représenté par m.
Exemple
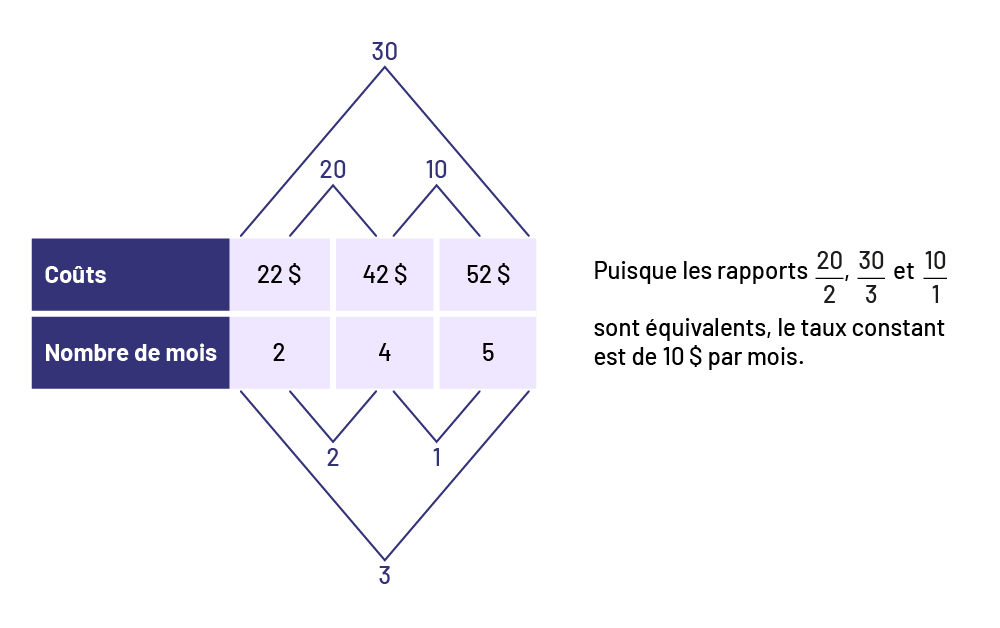
Source : En avant, les maths!, 7e année, CM, Algèbre, p. 3.
Connaissance : valeur initiale
La valeur initiale d’une suite croissante linéaire correspond à la valeur du terme lorsque le rang est zéro. Dans l’équation \( y = mx +b\) , la valeur initiale est représentée par b.
Exemple
Dans cette situation, la valeur initiale est de 15 $, puisque c’est la valeur de y lorsque x est à 0.
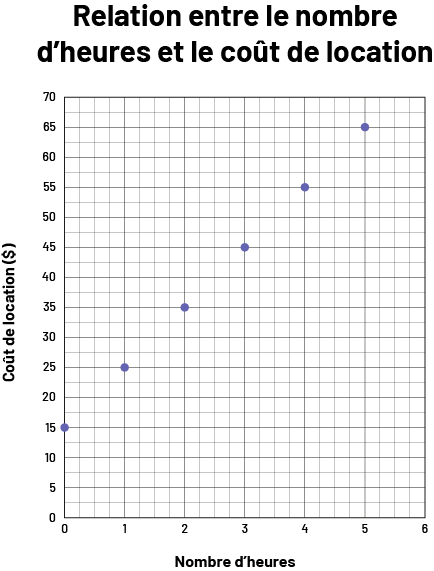
Source : En avant, les maths!, 7e année, CM, Algèbre, p. 4.
